Possiamo
supporre che la corona di cui parla Vitruvio,
avesse un diametro di circa 19 cm (corone con dimensioni di questo
genere sono state rinvenute in siti archeologici risalenti al periodo in
cui visse Gerone II). Per semplicità, supponiamo che il peso della corona
fosse di 1 kg, il suo volume, allora, è:
densità dell'oro: 19.3 g/cm3
Il volume di 1 kg di oro è pertanto:
(a) 1000 g/19.3 g/cm3 = 51.8 cm3
Il diametro della bacinella contenente l'acqua doveva essere almeno 20 cm (altrimenti la corona non avrebbe potuto esservi immersa) ; pertanto la sezione trasversale della bacinella ha una superficie di:
(b) πr2 = 3,14.102 =314 cm2
Immergendo la corona nella bacinella, l'acqua salirebbe di
(c) 51.8 cm3/314 cm2 = 0.165 cm.
Supponiamo che l'orafo disonesto abbia sostituito il 30% (300 g) d'oro con l'argento per fabbricare la corona;
densità dell'argento= 10.6 g/cm3
Il volume della corona costituita da oro ed argento è:
(d) 700/19.3 + 300/10.6 = 64.6 cm3
Immergendo la corona nella bacinella, l'acqua salirebbe di
(e) 64.6/314 = 0.206 cm
La differenza del livello dell'acqua nei due casi è soltanto
(f) 0.206 cm - 0.165 cm= 0.041 cm
Troppo piccola per poter essere osservata, soprattutto se si tiene conto degli errori sperimentali (acqua rimasta sulla corona, bolle d'aria intrappolate nelle decorazioni e così via).
Forse, come è suggerito nel sito dell'Università di Drexell, di Filadelfia 1 Archimede risolse il problema, utilizzando le leve e il concetto di spinta idrostatica per cui è tanto famoso.
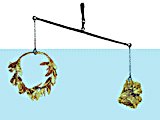
Archimede utilizzò uno strumento che prende attualmente il nome di bilancia idrostatica. Sospendiamo il chilo d'oro e la corona di ugual peso ai due bracci di una bilancia; in questo caso, evidentemente, la bilancia rimane in equilibrio e così rimarrà anche nel caso che i due oggetti vengano immersi in una vasca contenente acqua, se la corona è fatta tutta d'oro; se però la bilancia pende dalla parte della pepita d'oro (vedi figura), significa che la corona ha spostato una maggior quantità di acqua e pertanto la sua densità è minore; infatti,
se la corona è fatta per il 30%di argento, il suo volume è
64.6 cm3 (vedi f)
e quindi sposta 64.6 g di acqua, avendo l'acqua densità 1 g/cm3
e pertanto in acqua pesa 1000 g - 64,6 g = 935.4 g
mentre l'oro puro in acqua pesa 1000 g - 51,8 g = (vedi a)
Differenza che anche una bilancia semplice come quella a disposizione di Archimede poteva rilevare.
Galileo, influenzato dalla lettura di Vitruvio, costruirà la bilancia idrostatica, come si può leggere nelle pagine originali al sito: http://www.liberliber.it/biblioteca/g/galilei/la_bilancetta/html/bilancet.htm
1 Nel sito http://www.mcs.drexel.edu/~crorres/Archimedes/contents.html numerose informazioni, foto, animazioni sulle scoperte di Archimede e il suo tempo.