Einstein incontra Dante Alighieri

 

Riccardo Mansani

 

La realtà non è fatta a misura della nostra percezione e delle nostre capacità di comprenderla. Non c’è ragione che lo sia, visto che siamo noi a discendere dalla realtà e non viceversa. In questo senso la comprensione della realtà resta sempre, per noi umani, una sfida il cui successo non è scontato a priori.

Scienza è il nome che diamo a questa sfida, e sono a mio avviso stupefacenti, vista la premessa di questa breve introduzione, i risultati che, nel corso della storia umana, la scienza ha conseguito nel suo tentativo di consegnarci un’immagine della realtà sempre più adeguata alle nostre esigenze sia materiali che spirituali.

La scienza è attività logica che ci consente di dedurre, con rigore, verità non evidenti a partire da verità premesse. Ma la scienza è anche intuizione, sforzo di immaginazione, sintesi dei nostri input sensoriali, che ci permette di accedere, appunto, a quelle verità premesse del cui valore non possiamo rivendicare alcuna garanzia che non risieda in noi stessi, nella fiducia che riponiamo nei nostri apparati percettivi.

Frutto di intuizione sono quindi i nostri concetti primari come, ad esempio, le proprietà dello spazio nel quale ci sentiamo immersi. A questi concetti lo scienziato arriva elaborando più o meno consciamente, secondo un metodo non codificabile, i dati della sua percezione, ma agli stessi concetti, con lo sforzo della sua fantasia, può arrivare l’artista nel tentativo di piegare la realtà alle sue esigenze poetiche.

È il caso proposto dal fisico Carlo Rovelli nel suo saggio “La realtà non è come ci appare”, in un capitolo del quale vengono discusse le sorprendenti analogie tra la concezione dello spazio di Einstein e la struttura del Paradiso che Dante Alighieri descrive nei canti XXVII e XXX della terza cantica della Divina Commedia.

Proporre un estratto della discussione di Rovelli su questo singolare incontro tra Poesia e Scienza, ci è sembrato particolarmente adatto allo spirito della nostra rubrica.

(Riccardo Mansani)

 

Da “La realtà non è come ci appare” di Carlo Rovelli

 

“Due anni dopo aver pubblicato le sue equazioni, Einstein decide di provare a usarle per descrivere lo spazio dell’universo intero, considerato a scala larghissima. E qui ha un’altra delle sue idee strepitose.

Per millenni gli uomini si erano domandati se l’universo fosse infinito oppure avesse un bordo. Entrambe le ipotesi sono ostiche. Un universo infinito non sembra ragionevole: se è infinito, per esempio, da qualche parte c’è necessariamente un altro lettore come te che sta leggendo lo stesso libro (l’infinito è davvero grande, e non ci sono abbastanza combinazioni di atomi per riempirlo tutto di cose differenti l’una dall’altra). Ma se c’è un bordo, che cos’è il bordo? Che senso ha un bordo senza niente dall’altra parte?”

 

Dopo aver esaminato le difficoltà che le due ipotesi, spazio infinito e spazio limitato, avevano storicamente posto agli scienziati e ai filosofi, Rovelli prosegue:

 

“Ora, ragiona Einstein, in realtà possiamo salvare capra e cavoli: l’universo può essere finito e nello stesso tempo fare a meno del bordo, così come la superficie della Terra non è infinita, è finita, ma non c’è un bordo dove finisce.

Sulla superficie della Terra, se mi metto a camminare sempre dritto, non vado avanti all’infinito: torno al punto di partenza. Il nostro universo potrebbe essere fatto nello stesso modo: se parto con un’astronave e viaggio sempre nella stessa direzione, faccio il giro dell’universo e torno sulla Terra. Uno spazio tridimensionale fatto così, finito senza bordi, è chiamato “tre-sfera”.

Per capire come sia fatta una tre-sfera, torniamo un momento alla sfera usuale: la superficie di una palla, o la superficie della Terra.

Per rappresentare su un piano la superficie della Terra possiamo disegnare due dischi, come si fa abitualmente per disegnare i continenti (figura 1).

  

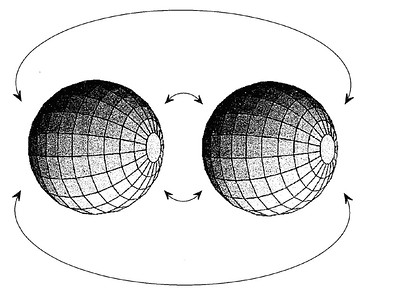 Figura 1, Una sfera si può rappresentare come due dischi incollati per il bordo

 

Si noti che un abitante dell’emisfero sud è in un certo senso circondato dall’emisfero nord, perché in qualunque direzione si muova per uscire dal suo emisfero arriverà sempre all’emisfero nord. Ma è vero anche il contrario ovviamente. Ciascuno dei due emisferi circonda e insieme è circondato dall’altro emisfero. Una tre-sfera si può rappresentare in modo simile, ma tutto con una dimensione in più: due palle incollate per il loro bordo che in questo caso è costituito dall’intera superficie di ognuna delle due sfere (figura 2).

 

Figura 2. Una tre-sfera si può rappresentare come due palle incollate per il bordo, dove il bordo è costituito dalla superficie delle sfere

 

Quando si esce da una palla si entra nell’altra (così come quando si esce da uno dei due dischi della rappresentazione del mappamondo si entra nell’altro), per cui ciascuna delle due palle circonda e insieme è circondata dall’altra palla.

La tre-sfera è la soluzione che Einstein propone al problema del bordo dell’universo, nel lavoro del 1917.”

 

La nostra intuizione non ci consente di visualizzare questo concetto, ma l’immaginazione umana ha potuto inventare una matematica con la quale è possibile gestire concetti di questo tipo senza particolari difficoltà: la sfera abituale è l’insieme dei punti in uno spazio a 3 dimensioni determinati dall’equazione: x² + y² + z² = 1. La tre-sfera è l’insieme dei punti in uno spazio a 4 dimensioni determinati dall’equazione: x² + y² + z² + u² = 1.

Esposta la concezione dello spazio di Einstein, Rovelli prosegue:

 

“Per quanto incredibile possa sembrare, la stessa idea era già stata concepita da un altro genio in tutt’altro universo culturale: Dante Alighieri. Nel Paradiso, Dante ci offre la sua grandiosa visione del mondo medioevale, ricalcata sul mondo di Aristotele, con la Terra sferica al centro, circondata dalle sfere celesti (figura 3)

 

 Figura 3. Rappresentazione tradizionale dell’universo dantesco

 

Dante risale queste sfere, insieme a Beatrice, nel suo viaggio visionario, fino alla sfera esterna. Quando vi arriva, contempla l’universo sotto di lui, con i cieli che roteano giù; in fondo, nel centro, la Terra. Ma poi guarda ancora più in alto, e cosa vede? Vede un punto di luce circondato da immense sfere di angeli, cioè un’altra immensa palla che, parole sue, “circonda e insieme è circondata” dalla sfera del nostro universo! Ecco i versi di Dante nel XXVII canto del Paradiso:

 

« Luce e Amor d'un cerchio lui comprende,
sì come questo li altri; e quel precinto
Colui che 'l cinge solamente intende. » (Par. XXVII, 112- 114)

 

E nel canto XXX, sempre sull’ultimo cerchio:

 

«Non altrimenti il trïunfo che lude
sempre dintorno al punto che mi vinse,
parendo inchiuso da quel ch'elli 'nchiude,
a poco a poco al mio veder si stinse » (Par. XXX, 10-13)

 

Il punto di luce e le sfere di angeli circondano l’universo e insieme dall’universo sono circondati! È esattamente la descrizione di una tre-sfera.

Le rappresentazioni usuali dell’universo dantesco, comuni nei libri di scuola, piazzano le sfere angeliche separate dalle sfere dei cieli. Ma Dante dice che le due palle circondano e sono circondate l’una dall’altra. In altre parole, Dante ha una chiara intuizione geometrica di una tre-sfera[1].

Il primo a notare che il Paradiso descrive l’universo come una tre-sfera è stato il matematico americano Mark Peterson nel 1979. in generale, ovviamente, i dantisti non hanno molta familiarità con le tre-sfere. Oggi, ogni fisico o matematico riconosce facilmente la tre-sfera nella descrizione dantesca dell’universo.”

 

A questo punto Rovelli si domanda come Dante abbia potuto concepire un’idea del genere e va a ricercarne l’origine nella sua formazione culturale. Da questa analisi nasce un’interessante osservazione: lo sviluppo di concetti più adeguati alla descrizione della realtà può essere bloccato dall’affermarsi di paradigmi che condizioneranno per secoli l’idea che ci facciamo del mondo. Nel caso specifico il paradigma in questione è la meccanica newtoniana la cui grandezza e importanza nello sviluppo della scienza non può essere messa in questione, ma che in questo caso svolse un’azione frenante nell’elaborazione di una visione del modo che, secoli dopo si rivelerà più adeguata.

 

“Come è possibile che Dante abbia avuto una simile idea che suona così moderna? Credo sia stato possibile, prima di tutto, grazie alla profonda intelligenza del nostro sommo poeta. È questa sua profonda intelligenza una delle sorgenti principali del fascino della Commedia. Ma anche grazie al fatto che Dante scriveva molto prima che Newton ci convincesse tutti che lo spazio infinito del cosmo è quello piatto della geometria euclidea. Dante era libero dai vincoli dell’intuizione che derivano dalla nostra educazione newtoniana.

La cultura scientifica di Dante era basata principalmente sugli insegnamenti del suo maestro e tutore, Brunetto Latini, di cui abbiamo un delizioso trattato, il Li Tresor, una specie di enciclopedia del sapere medioevale, scritto in un gradevole misto di francese e italiano arcaici. Nel Li Tresor Brunetto spiega nei dettagli il fatto che la Terra sia sferica. Ma lo fa -curiosamente, per un lettore moderno- in termini di geometria “intrinseca”, non “estrinseca”. Non scrive, cioè: “La Terra è come un’arancia”, come la vedrebbe uno che la guardasse da fuori; bensì scrive: “Due cavalieri che potessero cavalcare abbastanza a lungo in senso opposto si incontrerebbero dall’altro lato. E scrive: “un uomo che si metta in cammino e cammini per sempre, tornerebbe al punto sulla terra da cui è partito, se non fosse fermato dai mari”, e così via. Cioè si pone sempre da un punto di vista interno, non esterno. Il punto di vista di qualcuno che cammina sulla Terra, non di qualcuno che la guarda dal di fuori.

 

…………………………………………………………………………………………………………

 

 Ora, pensateci: per qualcuno che abbia imparato dal suo maestro che la forma della superficie del suo pianeta è tale che camminando sempre dritto si ritorna nello stesso punto, forse non è poi così difficile fare il passo successivo e immaginare che la forma dell’intero universo sia tale che, volando sempre dritto, si ritorni nello stesso punto: una tre-sfera è uno spazio in cui “due cavalieri alati che potessero volare in opposte direzioni si incontrerebbero dall’altro lato”.