Le geometrie dei Coleotteri Attelabidi

 

Piero Sagnibene

 

La geometria descrittiva ci permette di rappresentare su un piano gli oggetti dello spazio tridimensionale. Una delle sue rappresentazioni è l’evolvente del cerchio che  noi utilizziamo per costruire il profilo dei fianchi dei denti di una ruota dentata.

La costruzione geometrica dell’evolvente inizia da un punto che una circonferenza che ha in comune con una retta tangente (generatrice) che rotola senza strisciare sulla circonferenza deferente.

In forma parametrica le sue coordinate sono  x = a (cos t + t sen t)  ed  y = a ( sen t – t cos t). La semplicità della isometria di questa figura cela le difficoltà che essa sottende, e che a volte sono notevoli nelle sue applicazioni teoriche e pratiche. Ma se queste difficoltà, poniamo, riguardano uno studente normalmente dotato di un cervello con 100 miliardi di neuroni, allora, viene da chiedersi, come fa un piccolo insetto, con meno di un milione di neuroni, a realizzare praticamente il risultato di questa complicata costruzione, cioè di una evolvente su una foglia di Betulla? Eppure il piccolo insetto realizza l’oggetto tridimensionale di una evolvente immaginaria, ottenuta a partire da una circonferenza, anch’essa immaginaria, le cui linee di sviluppo (generatrici) sono, al tempo stesso, tangenti al cerchio e raggi dell’evolvente.

L’insetto però ha un vantaggio; lo studente in questione deve apprendere per via esogamica, elemento dopo elemento, le conoscenze necessarie, mentre l’abilità, la sapienza e la memoria “geometrica”, per così dire, dell’insetto sono state impresse dall’evoluzione nel suo DNA, nel corso della antichissima età biologica della sua specie, rispetto all’uomo, tempo durante il quale l’evoluzione ha operato selettivamente affinché quella specie acquisisse le facoltà necessarie ad ottenere questo risultato. Per l’insetto queste facoltà sono questione di sopravvivenza, il suo lavoro ha un unico fine: costruire un nido pedotrofico per le sue larve.

Vediamo allora come uno di questi insettini realizza il ricovero pedotrofico per la sua larva. Si tratta di un coleottero, un insetto olometabolo che, alla fine della sua vita larvale, deve impuparsi per trasformarsi in adulto, il Deporaus betulae, un Curculionide della famiglia degli Attelabidae (BILLBERG 1820) nota per comprendere anche altre  specie che  hanno le medesime attitudini ed abilità.

Il Deporaus betulae ha una predilezione per le foglie di betulla ma si adatta anche a quelle del nocciolo, faggio, pioppo, ontano. La femmina sale sulla pagina di una di queste foglie e, con le mandibole, esegue due tagli che partono rispettivamente dai due margini esterni ed opposti del lembo e coincidono medialmente sulla nervatura longitudinale. La prima linea di taglio disegna una S verticale, la seconda una S orizzontale ad inclinazione variabile, tanto più lunga quanto più la foglia è grande. Poi passa  sulla faccia opposta del lembo, ed, aiutandosi con le mandibole e con le zampe, arrotola la metà della foglia sulla prima incisione, in modo fa formare un cono lasso. Mordicchia quindi la superficie esterna dell’involucro, vi penetra e lo allarga comprimendone le spire. Poi fuoriesce ed inizia l’arrotolamento della seconda metà del lembo, che viene avvolta intorno alla prima, ottenendo una sorta di “sigaro”. L’estremità allargata del rotoletto viene chiusa piegando trasversalmente l’estremità distale della foglia. Quindi la femmina sigilla il tutto con una colla che solo lei è in grado di produrre. A lavoro compiuto la Depoarus intacca la parete del sigaro, ne solleva un porzione e vi introduce un uovo e, ripetendo la manovra più volte, introduce in ciascun rotolo 2-5 germi.

 

Esaminando le curve di sezione e comparandole con la forma e la grandezza della foglia, si giunge alla espressione matematica del lavoro dell’insetto. Gli assi di arrotolamento della superficie conica, che possiamo considerare come una superficie di rivoluzione, sono sempre rigorosamente tangenti alla curva inferiore della prima sezione ad S verticale. Queste tangenti risultano poi normali al contorno della foglia, e perciò il rapporto tra le due curve è quello che intercede fra una curva direttrice ed una curva in inviluppo (curva di sezione) funzione della direttrice (curva del margine fogliare). L’esistenza di un punto fisso per l’involucro interno  esige che la seconda sezione segni un seconda direttrice della curva di inviluppo, presentante le stesse costanti della prima e scostata da questa di un certo tratto. Lo spazio tra le due direttrici forma allora una superficie sferica che può avvolgere un cono intero.

 

 

 

Byctiscus betulae

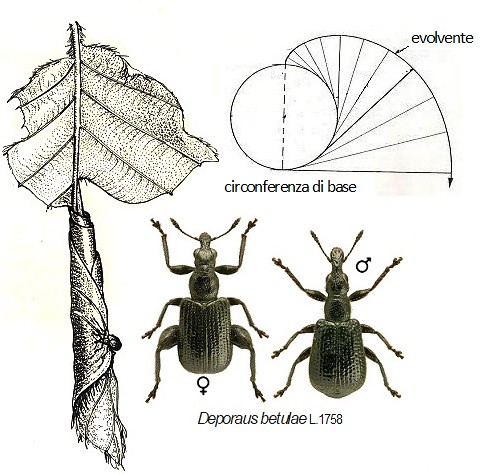
Rappresentazione dei principi geometrici fondamentali del taglio iniziale della foglia di betulla fatto da Deporaus. (a,b e c rappresentano il taglio).

 

Nella metà di destra della foglia è tracciato il cerchio ricavato dalla parte inferiore della curva ad S e xy è l’evolvente ottenuta da questo circolo. Le linee di sviluppo (le generatrici) dell’imbuto sono tracciate come rette. Esse, nella metà destra della foglia sono tangenti al cerchio xP. Una parte delle tangenti, segnate con linea sottile, raggiunge l’evolvente xy fra i punti P e P₁. Come si vede, le tangenti al cerchio sono, al tempo stesso, raggi dell’evolvente e sono perpendicolari all’imbuto.

Gli avvolgimenti degli imbuti esterni A,B,C, corrispondono simmetricamente agli avvolgimenti E,F,G degli imbuti interni. S=apice  della foglia, rappresentata con la  nervatura mediana distesa. (da Lengerken modif.).

 

La tecnica di fabbricazione del “sigaro” è comune ad altre specie di Attelabidi, ma nella famiglia vi sono specie che utilizzano, al medesimo scopo, tecniche anche diverse. L’Attelabus nitens, ad esempio, arrotola la foglia  in forma di cilindretto; esegue un taglio perfettamente perpendicolare alla nervatura centrale della foglia su metà della sua larghezza; poi taglia lungo la nervatura centrale in modo da eliminare quella parte della foglia e comincia il lavoro di arrotolarla seguendo precisamente il taglio della nervatura centrale. Il cilindretto deve essere cavo al centro per ospitare la larva, e la sua precisione è funzionale al corretto sviluppo di questa. Inoltre, il “sigaro” ha una doppia funzione; quella esterna, protettiva, per la quale i lembi di foglia esterni sono compressi, e quella interna dove i lembi di foglia sono meno costipati in quanto costituiscono il primo nutrimento per la larvetta.

 

Nel Byctiscus betulae, a primavera inoltrata (maggio), gli adulti, che hanno svernato nel terreno, emergono e si spostano sulle piante, nelle zone di foglie e germogli, sui quali le femmine praticano incisioni in attesa del periodo dell'accoppiamento . Gli alberi interessati sono, oltre le betulle, vite, pero, tiglio, pioppo, ciliegio e altre latifoglie. Si tratta di specie  praticamente innocue, che non danneggiano frutti o gemme. Le uova si schiudono dopo circa due settimane  le larve , apode e dalla tipica forma a “C” trovano da subito il nutrimento nelle pareti interne  del nido, nel quale di sviluppano. In estate, con la caduta dei loro rifugi a “sigaro”, le larve  completano la metamorfosi in adulti e si spingono nel terreno fino a 20 cm. di profondità con l’arrivo dell’autunno e vi restano fino alla fine dell’invero, superando così il periodo di gelo (svernamento). Con la ripresa vegetativa, la femmina raggiunge il maschio e pratica un foro all'interno del picciolo della foglia su cui si trovano, poi attende che si secchi, in seguito il maschio comincia ad arrotolarla perpendicolarmente al ramo dandole la particolare forma a sigaro, da cui deriva il soprannome della specie, per poi depositare centinaia di uova che, una volta schiuse, andranno a ripetere l'intero ciclo biologico.

Il vantaggio degli Attelabidi nell’utilizzare l’evolvente di un cerchio è data dal diverso modo di trasmettere la conoscenza da parte degli insetti e dell’uomo. La straordinaria abilità geometrica dell’insetto è ereditaria, non richiede apprendimento; al più deve adattarla alla diversità della foglia da utilizzare. Diversamente l’uomo deve imparare gradualmente grazie alla trasmissione alle generazioni successive, per via esogamica dei caratteri culturali acquisiti, un procedimento di tipo lamarckiano.