Uno scomodo bruco

Angiolo Innocenti 

Può, partendo da conoscenze elementari, emergere la soluzione di un problema che ha tenuto per anni impegnati studiosi di alto livello?

Ed è possibile che tale soluzione sia invisa per la sua semplicità, e venga tenuta

pressoché nascosta per una ostinata idolatria delle complicazioni?

Partendo da una stecca di legno, e da un’arte-scienza tra le più “terra-terra”, il

percorso che conduce fino ai segreti reconditi di una delle opere più grandiose realizzate dall’umanità.

“Un ti sgomenta’, bimbo” … non si trovava il doppio metro e c’era da misurare la lunghezza del campo. Lo zio Marino prese una canna, la mise per terra partendo dal filare di viti e, andando avanti rigirando il rudimentale strumento mentre io contavo, stabilimmo che il campo era lungo “27 canne”. Fu la mia prima lezione di agrimensura, quell’arte-scienza che avrei incontrato di nuovo qualche anno dopo, ormai adolescente e non più bimbetto di terza elementare, al corso per geometri.

Imparai, grazie a un contadino – anche i miei genitori erano stati contadini, ma ormai eravamo “de’ Bagni”, trasferiti a Montecatini praticamente mentre nascevo – una cosa che a scuola non ci avevano insegnato: il valore del tutto relativo dell’unità di misura, che è ininfluente, nel senso che se la cambi non cambia nulla, ai fini di una miriade di cose. Fu anche l’occasione per ripassare le frazioni: su due terzi del campo lo zio voleva provare a coltivare i cocomeri, perché era corsa voce che il terreno alluvionale delle aree costeggianti la Nievole in quella zona era adatto a tale coltura; ma d’altra parte non voleva rinunciare alle zucche, preziose per l’alimentazione dei maiali. Bene, 27 diviso 3 fa 9, che moltiplicato per 2 fa 18. I cocomeri su 18 “canne” di lunghezza del campo.

A fine estate, quasi tutti i cocomeri (che “sapean di poo”) sarebbero poi finiti nelle pille dei maiali, felici fruitori dell’ennesima conferma della validità del metodo sperimentale.

La 600 di Alvaro era vecchiotta ma ben tenuta, nonostante dovesse sopportare gli stivali motosi, l’inserimento a forza delle paline e il puzzo di sudore di chi, tramenandosi l’attrezzatura tra i filari di gelsi e i pruriginosi baffi delle pannocche del mais ormai maturo, stendeva la rotella metrica, traguardava con il tacheometro e picchettava … faceva, cioè, il lavoro del geometra, che, come fedelmente declama il termine, è il “misuratore di Terra” (ma anche di terra).

In realtà, il geometra fa anche tante altre cose, dalla pratica catastale al progetto della casa, dalla perizia per il mutuo al controllo del cantiere … e tante altre. Ma quella particolare porzione di professione – la parte topografica – era, secondo Alvaro, la più bella. “Arte-scienza”, perché chiamarla tecnica è riduttivo.

E fui sempre d’accordo con lui, andando a “tracciare” per la lottizzazione, per la divisione, per la nuova costruzione, quando d’estate, dalle medie in poi, mi chiamava piuttosto spesso ad aiutarlo. Ero il “canneggiatore”, figura essenziale nell’attività topografica “sul campo”; non solo portarobe, ma coadiutore a tutti gli effetti, perché la prontezza nel capire dove appoggiare la stadia, o dove piazzarsi perché chi è allo strumento veda meglio, o la scrupolosità nel piantare il chiodo sopra il picchetto, sono essenziali per la precisione e la speditezza del lavoro.

“Ti ricorderai di questi momenti come tra i più belli della vita”, diceva il navigato geometra al bastraoncello mentre, stanchi come muli da soma, si tornava sulla traballante vetturetta verso l’ufficio di Viale Balducci. Aveva ragione, e sapeva che sul sedile accanto c’era chi aveva già le idee chiare su cosa avrebbe fatto da grande. “Ma tieni presente che il topografo sul campo vien sempre guardato come uno sciaurato, perché la gente non capisce quello che sta facendo.”

A pensarci bene, il geometra è uno dei pochi mestieri che condivide il nome con un animale. E in effetti è più o meno come se tu fossi un vermetto, che ti guardano mentre giri per i campi con quegli attrezzi … stralunata diffidenza, e prima o poi ti vedi avvicinare il curioso che ti chiede. “ma che fate? e che ci vedete in quel canocchiale?”

Che gli rispondi? A quel punto ti accorgi quanto sia difficile spiegarglielo. Strano mestiere, quello del geometra. Basato, in fondo, su concetti semplici. Ma così difficile da spiegare.

Guerrino portava la spalla di maiale affettata “alla cannibala”, io il pane e il pecorino. Si trovava sempre un melo o una pianta di fico adattissimi per fare lo spuntino delle dieci e mezzo … niente di meglio dell’ombra di un fico, nelle torride giornate d’agosto. Guerrino è stato il miglior canneggiatore mai incontrato. Puntuale quanto spiritoso, baffetti e diastema alla Terry-Thomas e battutaccia sempre pronta, non so come avrei potuto fare senza di lui nei tracciamenti del ponte-viadotto all’Indiano e di quello del Varlungo. “Domattina si comincia alle 6, va bene?” … “Va bene, geometra, la si rihordi di pportare la rotella nova.”

Quando fai il tracciamento preliminare sei in piena campagna, e man mano che procedi ti duole il cuore a calpestare cavoli e insalata e a pensare che su una fascia di terreno larga una ventina di metri passeranno, di lì a un paio di settimane, le ruspe. Ti ritrovi a guardare con tenerezza quel fico che ora ti dà ombra e che chissà da quanto sta dando buoni frutti … e pensi all’agricoltore che per quattro palanche dovrà lasciare un patrimonio di secoli di lavoro e di genuina cultura, e andare a stare al settimo piano di un condominio a Novoli, per far posto a una strada di grande comunicazione. Poi ti ricordi che il progresso va avanti nonostante tutto e tutti, e non puoi che uniformarti a condividere le parole di chi disse che “le strade fanno conoscenza e la conoscenza fa strade.”

C’è, in questo lavoro, il crescendo di precisione. Qualche decina di centimetri di tolleranza nella fase preliminare, due o tre centimetri in quella esecutiva, e un paio di millimetri al massimo in quella di dettaglio. Qui occorre il massimo dell’attenzione, perché il punto dove pianti il chiodo sarà il centro del pilone, o della spalla del ponte … e poi c’è il patema d’animo perché tutto il lavoro che hai fatto vengono, alla fine, a controllartelo i Topografi. Quelli con la T maiuscola, con i primi strumenti laser, mentre tu hai lavorato con un vecchio teodolite Wild T2.

Penso di aver personalmente sperimentato, in quel periodo, uno dei pochi casi in cui ciò che ti è stato insegnato a scuola lo trovi perfettamente aderente alla pratica professionale. E quanto tu possa apprezzare una materia, fino addirittura ad amarla, quando hai avuto la fortuna di un insegnante eccellente come il professor Francesco Lacanà. Ed è proprio nel tracciamento di opere stradali che puoi trasferire tutto, tutto quanto, l’armamentario di nozioni di trigonometria … non si butta via proprio nulla!

Poi arriva la piena attività del cantiere, di cui sei chiamato anche a dirigere la parte operativa, e incontri un altro elemento della vasta serie di strumenti tanto utili quanto semplici: la modina.

Le modine sono ausili di tracciamento costituiti da tavole di legno. Vengono collocate sul terreno dal topografo di cantiere nella giusta posizione e con la giusta inclinazione  e,  una  volta  fornite  le  opportune  spiegazioni  al  caposquadra, permetteranno il corretto posizionamento delle opere. Per i bordi laterali degli scavi e per le scarpate dei rilevati si impiegano le modine triangolari: tre tavole formanti un triangolo rettangolo, con il cateto di base da appoggiare orizzontalmente a terra e con l’altro in verticale (quindi l’impiego di livella e/o filo a piombo è essenziale). Le lunghezze dei cateti sono tali da determinare una prefissata inclinazione dell’ipotenusa.

La modina triangolare rappresenta uno dei casi tipici nei quali l’unità di misura è ininfluente. Quel che conta è il valore della pendenza, definita come rapporto tra dislivello e proiezione orizzontale. Ad esempio per i rilevati stradali, che generalmente hanno scarpate con la pendenza 2/3, potremo usare indifferentemente modine con m. 1 di altezza e m. 1,50 di base, come di 60 cm d’altezza e 90 di base: qualsiasi dimensione, purché il rapporto sia quello.

Non è adatto al cantiere l’impiego dei valori d’inclinazione definiti con unità di misura angolari basati sulla suddivisione convenzionale dell’angolo retto in un numero n di parti. Nella pratica cantieristica devono operare in sintonia maestranze dei più diversi livelli di formazione, pertanto bisogna semplificare per ridurre al minimo le possibilità di fraintendimento. Al muratore che deve impostare muri e travi di appoggio del tetto di una casa non darai il goniometro prescrivendo che l’angolo del tetto sia di 16° e 70’, ma dirai semplicemente che deve avere la pendenza di 3 parti su 10, o del 30%, che è la stessa cosa. Lui alzerà di 30 cm per ogni metro in avanti sul solaio. Se ha perso il doppio metro a stecca, potrà usare qualsiasi altro oggetto, anche la sua scarpa: 10 scarpe in avanti e 3 in verticale, e la precisione è assicurata.

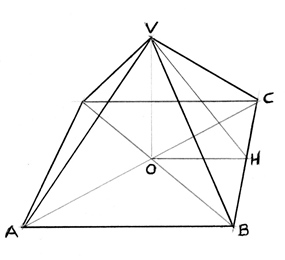Tra le tante costruzioni ardite realizzate dall’umanità, forse quella che ha dato luogo a più studi e discussioni è la piramide di Cheope. L’interrogativo “come avranno fatto?” ha forse superato in intensità e carica emozionale tutte le altre motivazioni d’indagine. Oltre al problema della cavatura, del trasporto e della collocazione degli enormi blocchi di pietra, c’è l’aspetto puramente geometrico: perché proprio quelle proporzioni, quei rapporti dimensionali? Una piramide regolare a base quadrata può essere più “schiacciata” o più “appuntita”, a seconda del rapporto tra l’altezza e il lato di base. Perché proprio quel rapporto? Uno potrebbe rispondere “è un rapporto come un altro; gli è venuta così, e basta” … ma la spiegazione non soddisfa, perché ci sono caratteristiche geometriche del tutto particolari. L’ “a casaccio” non è credibile, e quindi bisogna indagare.

Cosa c’è di tanto particolare? Supponiamo di sezionare la piramide con un piano che passa per il vertice e per i punti mediani di due lati opposti del quadrato di base. Ottengo un triangolo isoscele, che vado a dividere in due triangoli rettangoli uguali e speculari. Ne considero uno. Sapendo che il lato della base della piramide è m. 230,20 e l’altezza è m. 146,50, sto quindi esaminando un triangolo con il cateto di base di 230,20/2 cioè 115,10 e l’altezza di 146,50. Col teorema di Pitagora calcolo l’ipotenusa, che viene m. 186,30. A questo punto mi sbarazzo dell’unità di misura, che non ha alcuna influenza sulle proporzioni, attribuisco il valore 1 al cateto di base e scopro che il valore dell’ipotenusa è molto, molto vicino alla sezione aurea φ ≅ 1,618, col simbolo del “circa” giustificato dal fatto che si tratta di un numero irrazionale con infiniti decimali privi di serie ripetitive.

Interessante, questo fatto, anche se non ci si può meravigliare più di tanto perché la conoscenza del rapporto aureo era piuttosto diffusa nell’antichità. Il senso di armonia che infonde – basti pensare a quanto si riscontri in natura – lo fece adottare in varie forme artistiche. Gli antichi Egizi non avevano alcuna idea del concetto di “numero irrazionale”, mentre avevano molta dimestichezza con le frazioni. Probabilmente considerarono il 13 e l’8: ad entrambi questi numeri sono sempre stati attribuiti, un po’ in tutte le civiltà, significati particolari, e 13/8 fa 1,625, valore molto vicino al nostro φ.

Ma se le cose si fermassero qui! … il bello viene invece con lo scoprire la serie di proprietà particolari derivanti dal costrure una piramide con “dentro” quel bel triangolo. È qui che casca l’asino, perché lo stupore degli studiosi nel trovarsi tra le mani siffatte meraviglie, ha dato luogo alle ipotesi più intriganti; fino a generare, nei più fantasiosi, l’idea che conoscenze di livello superiore, inconcepibili per l’epoca, siano state trasmesse agli Egizi da extraterrestri capitati per una breve villeggiatura in quelle zone. Da qui, a immaginare poteri magici indotti da quella forma, il passo è breve.  Destò clamore negli anni ’60 la notizia che in America erano stati messi in vendita modellini della grande piramide egizia realizzati in materiale trasparente (c’era già il plexiglass?). Alti una quindicina di centimetri, avevano esattamente le stesse proporzioni di quella di Cheope, cioè non troppo ritte né troppo schiacciate … proprio la stessa proporzione. Perché? Perché c’era qualcuno che sosteneva che era quella proporzione a garantire poteri particolari all’oggetto: rilassante a guardarlo, elargitore di salute e sonni tranquilli a tenerlo sul comodino, e persino capace di affilare le lamette da barba che vi fossero state fatte stazionare una nottata (per i modelli dotati di base amovibile).

Ma vediamo, in sintesi, quali vere meraviglie matematiche sono riscontrabili in una piramide con quelle caratteristiche geometriche.

Partiamo da una sorpresa … che è sorpresa fino a un certo punto, in quanto diretta conseguenza della presenza di quel φ. Se andiamo un po’ a scorrazzare per la vasta letteratura tecnico-scientifica in materia, vediamo mettere ai primi posti questa … meraviglia … che è tale solo perché si è fatto un “giro pescoloso” (fuorviante) sin già dai primi passi, impostando i ragionamenti sulle misure anziché sui rapporti tra lunghezze. La “meraviglia” viene così enunciata: “La superficie di ciascuna faccia laterale della piramide ha un valore pari a quello del quadrato avente per lato l’altezza”. Bella scoperta, davvero! Noi non possiamo certamente restarne meravigliati, perché applicando il Teorema di Pitagora al “triangolo delle meraviglie” otteniamo che √ 1,618 = 1,272 che corrisponde al cateto lungo del triangolo e quindi all’altezza della piramide; il che vuol dire che il quadrato di 1,272 è 1,618 (apotema). E la superficie della faccia laterale è 2 x 1,618 / 2 quindi 1,618.

Veniamo a una meraviglia autentica. “Il perimetro di base ha la stessa lunghezza della circonferenza avente per raggio l’altezza della piramide”. Verifichiamo: 

Perimetro: 1 x 2 x 4 = 8

Circonferenza: ≅1,272 x 2 x π = 8

Questa è veramente una meraviglia: siamo di fronte al collegamento del tutto inaspettato e insospettabile tra due entità matematiche che apparentemente non hanno alcun legame tra loro: il numero irrazionale algebrico φ e il numero irrazionale trascendente π. Come diavolo può esser venuto fuori questo sposalizio? Diavolo della matematica! Diavolo dei “geni” egizi, che probabilmente ci si sono infilati dentro senza averne la più pallida idea! … come si può dar torto a chi volesse esclamare “è una specie di magia”?

In realtà (e qui si torna a quel discorso del φ ≅ 1,618 e del rapporto 13/8, vale a dire  alla considerazione che tutti i nostri ragionamenti, in questa sede, non pretendono, anzi rifiutano, la precisione rigorosa, ma danno la precedenza agli effetti pratici) non è “esattamente” così. Se nel calcolatore infiliamo i valori con un discreto numero di decimali, ci accorgiamo che la circonferenza non vale esattamente 8 (come invece è esattamente 8 la lunghezza del perimetro), ma è qualcosa come 7,9923352… Cosa voglio dire? Che quel che stiamo facendo, in tutto questo discorso, è un gioco di incastri che è meraviglioso proprio perché gli incastri funzionano bene indipendentemente dall’estremo rigore.

È un concetto che trova la forma piena nell’opera di Leonardo con i fondamenti della meccanica reale e funzionale. Entra in gioco il concetto di tolleranza (cioè “approssimazione controllata, di cui si fissano i limiti”). In sua assenza non potremmo neppure viaggiare in automobile. Con la “tolleranza zero” l’automobile non sarebbe realizzabile, e con tolleranze eccessive si sfascerebbe tutta dopo pochi chilometri. Principio, questo, valido in linea generale, non solo nella meccanica.

Sono diventato un disordinato e mi dispiace deludere chi mi chiede riferimenti bibliografici (mea culpa), ma di materiale in giro ce n’è in abbondanza. In rete c’è addirittura la sovrabbondanza, con immissione di dati, calcoli e teorie astruse che dimostrano molta più propensione per la numerologia di stampo astrologico che per la matematica. L’importante, pare, sia il convincere la gente che la questione è complicata al massimo dei gradi concepibili, e che l’intelligenza degli antichi Egizi era superiore al normale … dei “superdotati”, insomma, o per grazia divina, o per colloqui con i marziani, o sotto l’effetto di erbette reperite nei floridi campicelli dei dopo-inondazione. Tra le poche ipotesi serie mi è parsa interessante quella relativa alla figura della “Vesica Piscis”, che porta ad ottenere un triangolo con proporzioni molto vicine a quello che è il “cuore” della nostra piramide. Siccome ci si arriva con un procedimento totalmente grafico, ci sta. Invece non è giustificato, secondo me, il mettere in campo i valori angolari e le funzioni trigonometriche che – nel nostro caso – contribuiscono ad ingarbugliare ancora di più.

Può, allora, entrare in ballo la curiosità indotta nel geometraccio di cantiere da tutta questa roba. E può venir fuori una osservazione di quelle che fanno cascare le braccia a tutti i cultori di complicazione. Ci si è lambiccati il cervello per capire come avessero fatto a trasportare fin lì quegli enormi blocchi, e si sono anche spesi parecchi soldi per prove pratiche di simulazione, ma pochi si sono posti la domanda “se fossi stato il tecnico di cantiere, il geometra o il topografo o come diavolo si fosse chiamato là a quei tempi, come avrei fatto a spiegare ai capimastri il modo di piazzare quei blocchi di pietra nella posizione giusta per ottenere la forma giusta, cioè per rispettare il progetto?”

La  parte  pratica  della  faccenda:  la  cantierizzazione.  Convertire  l'idea  in disposizioni per le maestranze, realizzare l'opera. L’aspetto pratico non poteva venir messo da parte neppure nell’antico Egitto. Supponiamo che il nostro genio, la persona o l'equipe creatrice dell'idea, del progetto, si sia servito di un modellino in legno, in scala. Poi, sul terreno, abbia tracciato il quadrato di base. Una volta tracciata la base, come si poteva “tracciare” anche la posizione del vertice dell'opera, affinchè le proporzioni di progetto fossero rispettate? Mettendo, forse, un'asta verticale alta 146,50 m. (due volte e mezzo la Torre di Pisa) piantata nel punto di intersezione delle diagonali di base? Impossibile, inconcepibile.

C'è un solo modo per “cantierizzare”: farsi comandare dagli spigoli laterali, sia come direzione che come inclinazione. Andando su con precisione, il vertice sarà sicuramente raggiunto. La direzione si può seguire con esattezza estrema, una volta sistemati sul terreno riferimenti ben visibili all’esterno della costruzione, sui prolungamenti delle diagonali di base. Altrettanto agevole il rispetto dell’inclinazione, con uso di modine e con il rigore estremo nell’uso del filo a piombo. Quando metti la pietra angolare, devi assicurarti che sia spostata verso l’interno della piramide, rispetto alla “sorella” sottostante su cui ti appoggi, di un determinato valore.

Alcuni studiosi si sono resi conto che il metodo più pratico per passare dall'idea ai fatti è l'indicazione del valore dell'inclinazione. Però hanno focalizzato la loro attenzione sull'inclinazione della faccia laterale della piramide, presa sulla linea di massima pendenza, vale a dire sull'apotema. Le linee di apotema sono a metà dei lati di base, con una pendenza del 127 e rotti per cento. I problemi non mancano: collocazione scomoda per le operazioni pratiche, inclinazione troppo ripida, e valore aritmetico non frazionario difficile da replicare, disponendo solo di strumenti elementari. Ora come allora, l'obiettivo è sempre quello di ridurre al minimo le possibilità di errore, quindi le disposizioni da dare in cantiere debbono essere le più semplici possibile. I rapporti usati son sempre tra numeri interi; che, più piccoli sono, e meglio è.