Tra Matematica e Fisica una prospettiva interdisciplinare

 

Maria Arcà - Emiliano Degiorgi

 

Incontro di formazione rivolto a insegnanti di scuola secondaria di primo e secondo grado

 

AIRDM-UMICIIM L’insegnamento della matematica tra ricerca didattica e prassi scolastica 1 aprile 2022  

 

Elaborazione dell’ intervento 

 

Vi ringraziamo molto dell’invito. Io ci tenevo a partecipare anche perché, per mia esperienza professionale, non sono una matematica e mi incuriosiva entrare in un contesto diverso. Per questo, insieme a Emiliano Degiorgi, fisico e insegnante di scuola secondaria di primo grado, abbiamo cercato di capire come la matematica si mette in relazione con le altre discipline, ma anche come le tante discipline utilizzano necessariamente la matematica nella loro dimensione quantitativa, provando a metterci nei panni dei ragazzi che a scuola avviano la loro formazione matematica e scientifica. Non tanto dal punto di vista della quantità di conoscenze che riescono ad accumulare e sperabilmente a elaborare, ma dal punto di vista dei loro modi di guardare il mondo: come si costruiscono quei modelli mentali che sono così importanti per la costruzione di un pensiero scientifico? Cosa aspettarsi dalla matematica? Come l'insegnante riesce a capire quello che i ragazzi non capiscono, raccordando tra loro i vari problemi connessi al linguaggio, alle rappresentazioni scientifiche, alla vita abituale? Ci sembra che questo punto non venga particolarmente curato, né sia particolarmente presente nella letteratura e nei libri a cui i ragazzi fanno riferimento nel loro studio. Io ho lavorato moltissimi anni con il maestro Manzi e per lui era fondamentale “imparare a pensare”, il suo obiettivo era come insegnare ai ragazzi a pensare. Ci sembra che questo sia un compito che la scuola sta invece trascurando. È stato detto in una quantità di seminari come la parcellizzazione in unità didattiche all'interno di una stessa disciplina porti al nozionismo, e tutti abbiamo esperienza di come sul sussidiario un argomento sia presentato in una coppia di pagine e poi, a seguire, spesso si trovi un argomento non collegato o addirittura completamente diverso. Così, attraverso i libri di testo, la scuola di oggi presenta un sapere costruito attraverso i nomi delle cose più che attraverso le relazioni tra aspetti di un fenomeno da interpretare. Basta pensare all’elenco delle nomenclature biologiche che dovrebbero garantire la conoscenza del funzionamento del corpo umano, o ai nomi delle proprietà delle operazioni nelle prime classi di primaria, spesso non compresi dai ragazzi proprio a livello linguistico.

La scuola, poi, si impegna in una sorta di valutazione ossessiva con prove di ingresso e prove di uscita, poi di nuovo prove di ingresso nella classe successiva, prove a metà percorso… senza trovare più il tempo per insegnare o per parlare insieme di quello che si dovrebbe poi valutare. Sappiamo tutti, invece, che il pensiero ha bisogno di tempi lunghi per svilupparsi, ha bisogno di una sorta di processo che chiamiamo di metamorfismo mentale. Cioè, come nel metamorfismo geologico, le idee devono entrare in profondità nelle le teste dei ragazzini, mescolarsi con le altre e poi riemergere modificate, alterate; proprio come le rocce metamorfiche che riemergono trasformate dopo la loro permanenza nel sottosuolo.

Se andassimo a guardare le modalità dell'insegnamento e dell'apprendimento, potremmo trovare anche delle relazioni didattiche palesemente scorrette. C'è bisogno di onestà reciproca. Serve che gli studenti sappiano essere onesti in quello che dicono e in quello che capiscono, senza fare finta di sapere per compiacere l’insegnante. Ma moltissime/i insegnanti potrebbero essere molto più oneste/i nel loro insegnamento, cioè accorgersi che anche loro fanno finta di insegnare, quando quello che dicono diventa routine, prassi didattica per risparmiare tempo, disinteresse per i ragazzi e mancanza di impegno. È proprio la mancanza di onestà reciproca che rende il sistema scolastico così problematico e spesso così cervellotico.

Un altro punto che secondo noi viene trascurato, e che troviamo estremamente importante, è la cura del passaggio dal concreto all'astratto. Non si tratta di far fare esperimenti più o meno semplici ma di indicare come, attraverso varie attività, i ragazzi possano procedere nella costruzione di modelli esplicativi densi di significato, procedendo lentamente nel non facile lavoro di costruire conoscenza scientifica correlando il sistema dei fatti al sistema di pensiero. La conoscenza è invisibile e avere accesso all'invisibile vuol dire non fermarsi all’evidenza concreta ma, per esempio, immaginare relazioni tra eventi, sviluppare modi di collegare eventi, utilizzare strategie di pensiero causali o le tante strategie che guidano il pensiero e che sono necessarie per capire quello che ancora non si conosce.

A scuola si possono portare i ragazzi a sviluppare capacità di rappresentazione e modellizazione di fenomeni (quasi) quotidiani, imparando a pensare su cose da poco per riuscire poi a far crescere il pensiero sulle cose importanti. Bisogna sviluppare linguaggi capaci di esprimere questo pensiero, mentre sappiamo che le crocette dei test sono poco espressive da ogni punto di vista; ricordiamo che grandi pensatori e grandi filosofi ci hanno insegnato che “un modo di parlare è un modo di vivere”.

E se si parla male, probabilmente si capisce anche male.

Questo ovviamente è un problema importante a scuola.

Elaborare la costruzione di modelli è una delle più grosse difficoltà che i ragazzi si trovano ad affrontare, e le insegnanti non si accorgono di quanto la capacità di astrazione sia importante fin dai primi momenti di ogni apprendimento. Sembra che i modelli, o gli schemi, siano opera di grandi scienziati e non ci si rende conto che qualsiasi cosa che si arriva a conoscere, sia nella vita concreta sia nella vita scientifica, è sempre un modello di qualcos'altro: ogni modello di realtà corrisponde a un modo di pensare, a un modo di guardare il mondo. Dunque, la capacità di astrazione è un processo inevitabile, necessario per vivere, ma deve essere attentamente mediato dalla formazione scolastica.
Perché se si spera che questa capacità si sviluppi attraverso l’automatismo, nel modo mnemonico con cui si ripetono quotidianamente pensieri altrui, la competenza scientifica praticamente non viene acquisita. Certo, per padroneggiare bene le potenzialità delle varie discipline sono necessari anche esercizi un po’ noiosi, ma se uno sa a che cosa devono servire, si possono anche fare.

La necessità di fare modelli generali di realtà è difficile da comprendere, ma fin da piccoli si può cominciare a capire che quello che diciamo e quello che pensiamo sono astrazioni dai fatti, sono modelli dei fatti. I modelli assomigliano un po’ alla realtà ma non proprio tanto. Quando infatti, per caso o sviluppando nuove esperienze, gli scienziati si accorgono che la realtà dei fatti non si accorda più con i modelli generalmente accettati, bisogna immaginare nuove spiegazioni. Sono proprio le discrepanze tra quello che si osserva e le conoscenze organizzate a far progettare nuovi modelli e a far evolvere il pensiero scientifico.

E le stesse parole sono in realtà un modello degli oggetti a cui si riferiscono, rimandano all'idea delle cose e la costruiscono nei suoi tratti generali o particolari; ma le parole possono avere significati molteplici.

I grafici e i disegni sono delle ben strane rappresentazioni della realtà, eppure ne rappresentano esattamente certi aspetti.

La modellizzazione, non imposta didatticamente ma didatticamente costruita con attenzione e pazienza, diventa lo strumento chiave per ogni interpretazione scientifica. L’elaborazione di ogni modello richiede i suoi strumenti (da un fornello ad un microscopio elettronico…) le sue modalità di rappresentazione (una foto, un filmato, un grafico costruito matematicamente), le sue concettualizzazioni (misura, proporzionalità, andamenti, relazioni causali costruite sulla base di un semplice se… allora). È divertente pensare che mentre tutti si immaginano che la scienza si occupi di fatti e fenomeni concreti, in realtà la scienza si occupa di dare interpretazioni e rappresentazioni astratte dei fatti concreti; e non bisogna confondere la rappresentazione con la realtà.

Per capire questo ci vuole studio, attenzione e pazienza. Ed è importante anche fare il passaggio inverso: attraverso il modello, attraverso il grafico che realtà si riesce a vedere? Io certe volte immagino che attraverso il modello si riescano a vedere, come in trasparenza, aspetti di realtà, e che sia così possibile rivedere, seppur deformati, i fenomeni cui il modello si riferisce e le trasformazioni che li coinvolgono. Il progressivo passare dal visibile al mentale e dal mentale al concreto visibile è un'operazione concettuale molto delicata, molto raffinata. Ma per la scuola occuparsi di questo sembra proprio una perdita di tempo. Proprio per la loro parzialità i modelli possono imbrogliare: come si fa ad accorgersi che un modello non rappresenta quello che sembrerebbe ovvio e, solo guardando meglio, ci si accorge che rappresenta un'altra cosa? I possibili errori di interpretazione danno un'idea di come, a volte, si prende la rappresentazione semplificata come se fosse la realtà, dimenticando che nella realtà c'è una profondità e una vastità di sguardo che la rappresentazione non riesce a mettere in evidenza.

Nel delicato processo di formazione, l’impegno comune delle discipline è quello di aiutare i ragazzi a capire e a pensare, a elaborare modelli personali che potranno confluire in più complessi modelli scientifici. Bisognerà rendersi conto della varietà e qualità delle interazioni/relazioni che legano un evento ad un altro, immaginare strutture in cui sia possibile individuare lunghe o brevi catene causali, trovare linguaggi o altre modalità di rappresentazione per renderle evidenti a chi non è ancora capace di vederle. La semplificazione è utile solo quando ci si rende conto che ogni modello – ogni esperimento – è solo un piccolo ingrandimento di un frammento selezionato di un quadro molto più complicato. Così in biologia la fragilità e la complessità del sistema vivente non può essere ridotta ad accurate nomenclature dell’apparato digerente ma può meglio essere rappresentata dalle relazioni tra diversi livelli di complessità; o le caratteristiche fisiche del moto senza attrito, straordinariamente al di fuori di ogni esperienza, non possono essere ridotte ad una semplice rappresentazione grafica ma possono (e devono) essere corroborate dalla percezione corporea del movimento.

Gli specifici “modi di guardare il mondo” delle diverse discipline portano a diverse modalità di modellizzazione, ma al fondo resta sempre quella che è in realtà una speranza. Si spera cioè che possa esistere un modello comprensivo, un modello totale che possa rappresentare “tutto”.

Invece i modelli sono frammentari e parziali, e di solito riguardano pezzettini, aspetti dei fatti; questa è la differenza infinita tra il modello e la realtà. Sono state dette molte frasi significative (che talvolta sono diventate luoghi comuni) tipo “la mappa non è il territorio, il territorio non è la mappa”, che indicano complessivamente che la rappresentazione non è la realtà. Eppure, anche parlando, passiamo continuamente dall’astratto linguistico al concreto fattuale, e questo funziona, perché sappiamo bene come non prendere la realtà per la sua rappresentazione o la rappresentazione per la sua realtà.

Provate a pensare alle esperienze di galleggiamento fatte con i bambini: come è possibile immaginare di pensare che, mettendo un pezzo di pongo nell'acqua, si riesca a capire come mai navi immense galleggiano e che, nella loro immensità, galleggiano così bene. Come fa il pezzettino di pongo non completamente appiattito a rappresentare la nave, come fa il pezzettino di pongo che non va a fondo ad essere un modello che fa capire come la nave non vada a fondo, e “dimostrare” che la ragione di questi due galleggiare è sostanzialmente la stessa. L’efficacia del modello è abbastanza importante. L’esigenza epistemologica dell'insegnante porta non solo a conoscere e analizzare le esperienze concrete, ma a sviluppare sensibilità e conoscenza per capire cosa non si capisce, per capire come i ragazzi non capiscono.

Bisognerebbe ragionare sulla dialettica tra capire e non capire e su come, a partire da esperienze piccolissime e parziali, si possa costruire una conoscenza auto consistente di vasto potere interpretativo, e non sia frammentata come i dischetti di legno nel sacchetto della tombola, che sopra hanno tutti dei bellissimi numeri ma tutti perfettamente indipendenti l'uno dall'altro. L’aver cura del pensiero non vale solo per i bambini piccoli. Vale anche per la scuola superiore, con persone che sembrano grandi e ragionevoli. È necessario che la scuola, oltre a istruire, abbia cura del modo di pensare dei ragazzi, abbia cura delle loro idee, del loro sviluppo di conoscenze, dando loro la possibilità di trasformare le cose che vedono, che leggono, o che fanno in un sapere più ampio e comprensivo, che serva effettivamente nella vita per rendersi conto dei fenomeni del mondo. Certo, le discipline sono diverse ed è importante che ognuna abbia la sua competenza specifica, però è anche importante riconoscerne le sovrapposizioni e le intersezioni, sia metodologiche sia nelle strategie cognitive di base, per non dare ai ragazzi un'immagine di mondo frammentario e scoordinato.

Dei ragazzini di 4^a elementare rappresentano con disegni il loro modello di aria. Spesso si dice che siccome l'aria è invisibile, i ragazzini non possono neppure immaginarla.

Guardate invece che c’è chi la immagina in particelle divise, o chi ne immagina una struttura complessa: le particelle sono legate tra loro non con ganci ma con fili quasi invisibili, formando una rete continua. Il fatto che l’aria sia invisibile è indicato, in tutti i disegni, con il simbolo della lente d'ingrandimento, perché i bambini sanno bene che bisogna ingrandire molto quello che non si vede. (fig. 1)
Quindi se ragazzini di 4^a elementare sono capaci di vedere “l’invisibile”, è importante che questa capacità non venga perduta.

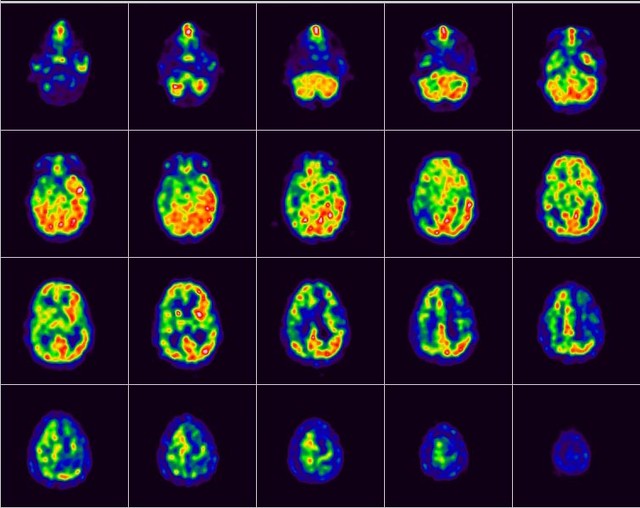
Studi di neuroimaging mettono in evidenza le zone in cui si verificano le attivazioni cerebrali in relazione a stimoli controllati. (fig 2)

Quindi ci si potrebbe domandare, provocatoriamente, se sia possibile far sviluppare, attraverso l'insegnamento, le macchie che rappresentano la risposta del cervello al pensiero scientifico e alla matematica. Perché se non si sviluppano le macchie e ci si ferma soltanto alle parole o alla ripetizione del sussidiario, il discorso resta sterile e si dimentica facilmente mentre, se si sviluppa una macchia, probabilmente la conoscenza resta più stabile, soprattutto più integrata con le altre e più significativa. 

La matematica si propone come un sistema che faccia da ponte tra discipline diverse e quindi deve inventare sistemi simbolici che colleghino i diversi aspetti del mondo. Però, secondo me, alcune cose devono essere molto esplicitamente chiarite. Che cosa viene veramente simbolizzato, per esempio nel conteggio, e come si riesce a capire che certi simboli rappresentano azioni di vita quotidiana? Forse fin dalla scuola dell'infanzia molti significati potrebbero essere approfonditi con maggiore cura.
I fisici modellizzano per mezzo di grafici, su piano cartesiano, alcuni aspetti di realtà, i chimici usano altri formalismi, e i biologi altri ancora. Si possono guardare le differenze e le somiglianze cercando modalità di contaminazione e sovrapposizione tra le diverse discipline soprattutto ragionando su come vengono rappresentati cambiamenti e trasformazioni. In un modo o in un altro i modelli permettono strategie di confronto tra i diversi “succedere” dei fenomeni, e per capire meglio è importante non solo ragionare sui diversi contenuti disciplinari ma, soprattutto, sulle strategie che servono per interpretarle. Si possono di volta in volta privilegiare strategie di confronto oppure strategie di relazioni causali. Come scegliere? Come fanno i fisici a individuare le variabili importanti? Nel percorso didattico è importante capire cosa guida le scelte: i modi di guardare un fenomeno portano a scegliere le variabili che devono essere considerate, mentre molte altre devono essere trascurate.

A partire dalla percezione delle qualità /proprietà degli oggetti, fin dalla scuola dell’infanzia, si può gradualmente costruire l’idea di variabile in senso fisico, e qui, secondo me, possono cominciare le difficoltà dei ragazzi.

 

I passaggi che portano dalle percezioni alla misura sembrano facili, ma non è proprio così. Tra l'altro esistono misure che non sono solo misure di lunghezza (quelle privilegiate didatticamente), e non sempre a scuola si lavora sulle misure di peso o (in casi molto raffinati) su misure di trasparenza o di luminosità. C’è a monte il problema generale di come si danno numeri alle variabili (lunghezze e non lunghezze), e come si passa dalla misura alla rappresentazione dei dati sullo spazio. Si deve riuscire a capire il significato della formalizzazione, e capire come la matematica permette di mettere in evidenza la forma dei fenomeni. Per esempio, è possibile cominciare a rappresentare la variabilità delle variabili, dando una forma simbolica alle semplici percezioni di più e meno, di maggiore di… o minore di.. sia in senso statico (è di più) o in senso dinamico (diventa di più). Lo spazio di un foglio diventa il grande palcoscenico su cui le variabili rappresentano le loro relazioni, è lo sfondo per i modelli iniziali. Per cominciare, semplicemente alzando o abbassando le mani (con i gesti di un direttore d'orchestra per variabili) si può indicare come la variabile diventi -di-più o diventi-di-meno; poi a questi cambiamenti si possono far corrispondere segni grafici, prima soltanto arbitrari e poi sempre meglio definiti, strutturandoli attraverso misure e infine rappresentandoli su un piano cartesiano. (Fig. 3) Queste sono forme date da bambini al cambiamento della fame durante la giornata e al cambiamento dell’arrabbiatura della mamma durante la giornata. Si comincia con forme semplici, che rappresentano con evidenza un crescere e un diminuire nel tempo, ma bisogna gradualmente orientare pensiero e rappresentazioni a passare da andamenti temporali ad andamenti causali.

 

Si dice che il piano cartesiano rappresenta uno spazio astratto, ma come si costruisce uno spazio astratto? Cosa significa? Sì, per ricordare una esperienza che si immagina condivisa dai ragazzi si dice che è un po’ come a battaglia navale solo che sono punti invece che quadretti…. O cose del genere. Come si fa a capire se i ragazzi hanno capito il significato potente di questo tipo di rappresentazioni? Alcune domande potrebbero mettere in evidenza importanti difficoltà di base, aiutando gli insegnanti a riflettere se, nella loro pratica, riescono a superarle.

Che cosa sono gli assi che rappresentano le variabili?

Com’è possibile immaginare che una variabile sia un asse?

Com’è possibile immaginare che cosa rappresentano i punti nello spazio?

 

Com’è possibile che la continuità di una linea rappresenti l’andamento di un fenomeno?

E poi, come fa una linea su un piano (sia pure speciale) a rappresentare l’andamento di una variabile in funzione di un’altra variabile (compreso il tempo)?

Molte cose vengono troppo spesso date per scontate in maniera superficiale ma è su queste che il pensiero dei ragazzi poi spesso si blocca, o cade nelle procedure di soluzione automatica.

È anche importante prendere spunto da quello che i ragazzi sanno benissimo, che è parte della loro esperienza, e trasformarlo in concetti interpretativi potenti. Riflettiamo ancora una volta sulle parole. I bambini anche piccolissimi dicono: più tiro l’elastico più si allunga. L’insegnante sa vedere in questo un abbozzo di pensiero proporzionale trasformando questa frase in: se tiro poco si allunga poco, se tiro di più si allunga di più, trovando correlazione causale tra il tirare e l’allungarsi? E con i più grandi si può ancora trasformare l’esperienza in una specie di esperimento per vedere se è vero che: se metto peso “uno” l’elastico si allunga di un po’ e se metto peso doppio l’allungamento potrebbe essere doppio. La costanza dei modi di succedere, trasformata in tabella e poi in grafico, contribuisce a visualizzare la proporzionalità tra peso e allungamento, la formalizzazione permette di vedere la forma dell’allungamento. E a scuola sono innumerevoli e necessarie le possibili proposte di esperienza-esperimento in cui lo stesso “modo di succedere” dei fatti può essere ritrovato e sovrapposto (sia come concettualizzazione che come formalizzazione) a quello visto per pesi e allungamenti. 

 

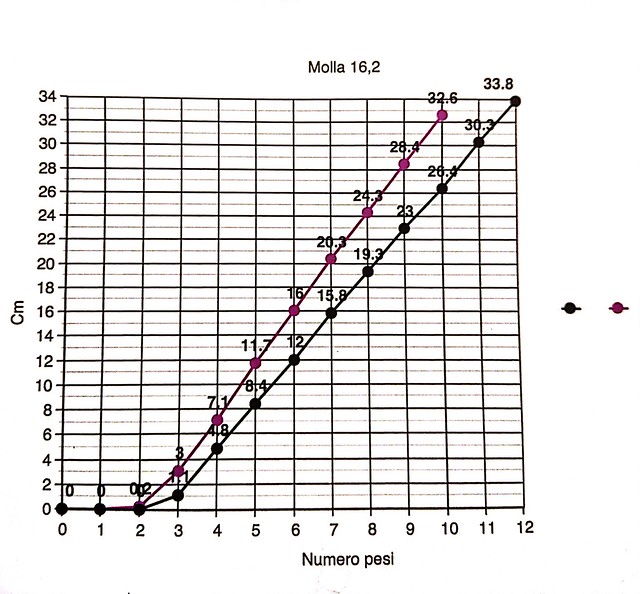L’idea che le forme matematiche rappresentano le forme del succedere degli eventi è veramente importante, anche se non è affatto evidente come una rappresentazione matematica possa rappresentare un aspetto di realtà. Attraverso una varietà di esperienze si riesce a vedere (e a capire) che una stessa forma di linea su un piano spazio-tempo può rappresentare un modo di camminare, su un piano peso-volume rappresenta un modo di galleggiare, su un piano tempo-panini rappresenta la fame durante la giornata. Si stabilizza così un’idea di pensiero proporzionale, attraverso un grafico capace di descrivere una varietà di fatti diversi. La retta sul piano non riguarda la loro diversità (a questo pensano le coordinate) ma il loro stesso modo di succedere. E questa è una delle concettualizzazioni più importanti che la scuola possa dare ai ragazzi. (Fig. 4) 

In sintesi, la formalizzazione matematica permette di mettere in evidenza una stessa forma di comportamento in fenomeni diversi studiati nella loro specificità da discipline diverse. Non si tratta di banalizzare in esercizietti le relazioni tra fisica e matematica, tra matematica e biologia, tra biologia e fisica e chimica… e storia, e epistemologia… ma di uscire dallo specifico disciplinare per costruire su basi matematiche delle modalità interpretative per alcuni (pochi o tanti non si capisce) aspetti del mondo.

Concludiamo ribadendo la necessità di imparare a pensare, sul fatto che ci sono idee grandi che possono connettere i vari saperi disciplinari, che ci sono modi di ragionare comuni a diversi contesti, che ci sono strategie cognitive utili per comprendere le diverse situazioni e che su questi “dati di fatto” la scuola può costruire un sapere stabile, intelligente e, soprattutto, capace di crescere ed espandersi in conoscenze più ricche e più comprensive.