La matematica come un gioco
Ogni gioco è un misto di vari ingredienti:
un po’ regole, un po’ fantasia, anche competizione, caso, travestimento, vertigine. (1)
Le Indicazioni per il curricolo, con riferimento alla Matematica, sottolineano il ruolo cruciale del gioco nell’educazione.
E’ fondamentale il laboratorio “in cui l’alunno è attivo, formula le proprie ipotesi e ne controlla le
conseguenze, progetta e sperimenta, discute e argomenta le proprie scelte, impara a raccogliere dati, negozia e costruisce significati, porta a conclusioni temporanee e a nuove aperture la costruzione delle conoscenze personali e collettive.”
Intorno a questi aspetti dell’insegnamento vengono proposti alcuni stimoli, senza la pretesa di ritenerli novità, in attesa dei contributi dei lettori.
(1) Da P. A. Rovatti, D. Zoletto, LA SCUOLA DEI GIOCHI, Tascabili Bompiani
Matematica 0-6 ∞ Un progetto di ricerca-azione sulle strutture aritmetiche nella scuola di base ∞ Problemi per matematici in erba ∞ SPECCHI ∞ Mathup I Corsi ∞ Math Result Quaderno a quadretti Tesi di Laurea in didattica della Matematica di Pezzia ∞ Progetto didattico: La ballata degli elefanti ∞ Commento “matematico” a La ballata degli elefanti ∞ La storia di Martina e il Gigante ∞ Problemi di Gioele il pastore ∞ La bella Kadija dagli occhi blu ∞ Non solo far di conto ∞ Rapporto e proporzione in situazioni di fittezza ∞ La calcolatrice ed il “far di conto” ∞ La matematica come gioco ∞
Quale educazione matematica al nido e all'infanzia?
Lucia Stelli
Abstract
Il libro "Matematica 0-6" curato da Maria G. Bartolini Bussi, professore ordinario di Didattica della Matematica presso l’Università di Modena e Reggio Emilia, e due coordinatrici pedagogiche, Patrizia Rilei e Francesca Botti,costituisce un’autentica novità nel panorama della ricerca in didattica della matematica. Raccoglie i principali risultati di un processo di ricerca-formazione realizzato in un periodo di sei anni presso nidi e scuole dell’infanzia del Comune di Modena e chiarisce come si possa parlare di matematica quale sapere da insegnare nel segmento 0-6.
Frutto di un lavoro collettivo, il libro "Matematica 0-6” , edito da De Agostini Scuola, fa parte della collana "Nuove Convergenze"curata dall'Unione Matematica Italiana (UMI) e la sua Commissione Italiana per l'Insegnamento della Matematica (CIIM). E’ pertanto un prezioso contributo alla qualità del fare scuola , rivolto principalmente agli insegnanti del nido e dell’infanzia. Vengono infatti forniti dispositivi concettuali e paradigmatici teorici per proporre contesti di apprendimento e scoperta in modo non casuale e pervenire a una progettualità sempre più intenzionale, tesa a integrare, armonizzare e valorizzare esperienze tradizionalmente considerate come percorsi separati dei due servizi .
La figura di insegnante che viene a delinearsi è quella di un professionista in campo educativo, che indipendentemente dal fatto che lavori nello 0-3 o nel 3-6, ha un atteggiamento di ricerca e si pone domande che gli consentono di leggere e interpretare i processi che i bambini compiono. Al contempo è in grado di raffinare la propria conoscenza sull’infanzia per riprogettare in un’ottica di continuità i contesti di scoperta dei bambini e le possibili piste di indagine che li accompagnano.
Tutto il percorso formativo si basa su una doppia solidità scientifica, quella teorica della ricerca universitaria e quella esperienziale di sperimentazione di pratiche in contesti educativi.
Proprio per mettere in relazione questi due aspetti la professoressa Bartolini Bussi illustra nel primo capitolo del libro il modello teorico Vygotskiano della mediazione semiotica alla base del processo di insegnamento-apprendimento.
Il sostantivo mediazione si riferisce ad un processo che include i seguenti partecipanti e circostanze:
1. qualcuno che media, il mediatore;
2. qualcosa che viene mediato, il contenuto della mediazione;
3. il ricevente a cui la mediazione apporta qualche differenza;
4. la circostanza della mediazione;
5. i mezzi della mediazione, la modalità;
6. il luogo in cui la mediazione può avvenire.
L’aggettivo semiotica si riferisce invece al processo di interiorizzazione che ha la propria base nell’uso dei segni, principalmente il linguaggio naturale ma anche ogni tipo di segni, dai gesti a quelli più sofisticati del linguaggio matematico.
Al centro della mediazione semiotica sta l’artefatto. La parola artefatto in matematica evoca strumenti fisici dell’aritmetica e della geometria ad alta manipolabilità. Sono esempi di artefatti gli ambienti virtuali, i testi e oggetti fisici quali le dita, il Lego Duplo, il pallottoliere gigante, il robot Bee-Bot, i calendari…
Testo completo 5 pg con illustrazioni
__________________________________
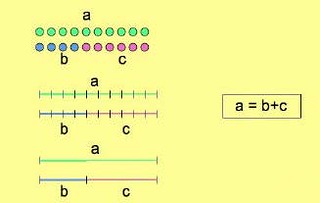
Un progetto di ricerca-azione sulle strutture aritmetiche nella scuola di base
Maria Mellone & Maria Pezzia ()
“pareva non potesse pensare se non con le mani”
(U. Eco, Il nome della rosa)
Introduzione
Nell’ambito dell’educazione matematica l’origine della comprensione delle operazioni aritmetiche nei bambini è da sempre una delle questioni più discusse; con il tempo si è fatta strada l’idea che tale origine sia da ricercare negli schemi di azione. Questa ipotesi ha giustamente trovato largo consenso nelle moderne teorie di apprendimento (Correa, Bryant & Nunes, 1998), tuttavia è fondamentale operare in modo tale che detti schemi non entrino in conflitto con le fasi successive di costruzione delle operazioni, ostacolando in tal modo la possibilità di predisporre, fin dai suoi stadi iniziali, un programma di matematica organico. Vi è quindi la necessità di costruire nelle scuole elementari un approccio all’aritmetica che tenga in considerazione sia le sue radici negli schemi di azione, che i successivi passaggi di sviluppo.
In questa direzione il nostro lavoro di ricerca si sviluppa attraverso la coordinazione di un progetto sperimentale presso la scuola elementare Madonna Assunta, 73° circolo di Napoli e una prima. Nell’azione di ricerca, iniziata nel 2003/2004, stiamo seguendo una classe elementare dalla prima alla quinta, cercando in collaborazione con l’insegnante di creare “dinamiche di risonanza”1((*C*)) ed osservarne il funzionamento. Siamo al quarto anno ed i primi risultati, riportati in (Guidoni; Mellone & Pezzia, 2005), e il lavoro di ricerca attualmente in corso ci fanno pensare che nell’insieme “la cosa funzioni”: le attività proposte, il modo in cui vengono sviluppate, le relazioni tra le persone coinvolte concorrono effettivamente a creare dinamiche di “comprensione risonante”. Spiegheremo meglio in seguito su quali elementi ci basiamo per poter fare questa valutazione. In questo momento stiamo tentando di dare una più precisa sistemazione teorica alle osservazioni e riflessioni emerse nel corso del progetto. Il nostro lavoro ha l’obiettivo di chiarire meglio quali sono i punti di forza della situazione sperimentale in cui siamo coinvolte, e quali i “punti critici” in cui è necessario che l’opera di mediazione culturale svolta dagli adulti si faccia particolarmente attenta e sensibile alle difficoltà che prevedibilmente incontreranno i bambini. Rispondere a queste due domande è essenziale per proseguire la sperimentazione nella direzione migliore e soprattutto per poter pensare di allargarla ad altri contesti. In particolare come formatori di insegnanti ci poniamo quotidianamente il problema di come l’esperienza maturata in progetti sperimentali come questo possa essere comunicata e utilizzata dai maestri o futuri maestri. Spesso il pericolo è che gli insegnanti rimangano con la convinzione di dover prendere un pacchetto di attività preconfezionato e “collaudato” dai ricercatori, e semplicemente applicarlo (Vaccaro, 2005). Procedendo in questo modo è ben difficile che i risultati siano positivi. Le condizioni che hanno reso possibile la comprensione in una situazione didattica non sempre sono i fattori più evidenti ad un primo sguardo, e si rischia quindi di riprodurre soltanto alcuni aspetti inessenziali, superficiali di una determinata attività, che potrebbero e dovrebbero invece essere modificati per adattarli ad un contesto differente. Nel far questo spesso si trascurano proprio i reali punti di forza del modello di intervento proposto, non si arriva a capire quello che realmente una certa esperienza può insegnare.
Testo completo 20 pg con illustrazioni
Problemi per matematici in erba
Sofia Sabatti (*)
L'articolo che qui rilanciamo è apparso su MaddMaths!, blog patrocinato da SIMAI, UMI e AIRO.
Abstract Da pochi mesi è online Problemi per matematici in erba. È un sito “in evoluzione” che si propone di raccogliere problemi “belli”. È uno strumento che speriamo sia utile per quegli insegnanti che vogliono promuovere la comprensione, attivare processi di pensiero nei loro alunni, suscitare in essi il gusto per la ricerca e la scoperta e che siano convinti che la maniera naturale per avvicinarsi a questi obiettivi sia quella di far confrontare i ragazzi con problemi significativi.
Che cos'è problemi.xyz Problemi per matematici in erba è un sito dinamico: i contenuti in esso presenti vengono aggiornati senza una particolare periodicità, ma per il momento abbastanza frequentemente (almeno un paio di volte al mese). È un blog, nel quale gli insegnanti sono invitati a lasciare i propri commenti ai problemi presentati (soluzioni alternative a quelle proposte, difficoltà riscontrate nel proporli alle classi, segnalazioni di errori, risultati particolarmente positivi...). È uno strumento didattico gratuito: qualunque insegnante può accedervi e utilizzare nella propria scuola le risorse in esso contenute. (continua)
Math Result è un prodotto innovativo per imparare la matematica, frutto delle più avanzate competenze del mondo Pearson nella didattica disciplinare e nei format digitali per l’apprendimento. Il progetto è nato dall’incontro di Pearson Italia con il team di Lab51, specializzato nello sviluppo di software di matematica, e si è avvalso di un gruppo di autori portatori di una solida esperienza nella didattica della matematica.
Imparare è un bellissimo viaggio, facciamolo insieme
Il gruppo di lavoro che si occupa di questo sito è composto da docenti di matematica a vario livello. In particolare:
- docenti di scuola primaria, di scuola secondaria di primo grado e di scuola secondaria di secondo grado che fanno riferimento al "gruppo di ricerca sulla didattica della matematica nella scuola elementare" del Dipartimento di Matematica "F. Enriques" dell'Università degli Studi di Milano;
- personale universitario afferente a diverso titolo alle unità di Milano-Città Studi e Milano-Bicocca del Centro matematita, impegnati nella prima formazione e nella formazione in itinere degli insegnanti di scuola primaria e secondaria.
Laboratorio di matematica: una sintesi di metodologie e contenuti
Maria Dedò, Simonetta Di Sieno
In questo articolo ci proponiamo di tirare le fila di dieci anni di sperimentazione, da parte
del centro “matematita”, della modalità laboratoriale a tutti i livelli dell’insegnamento /
apprendimento della matematica, analizzandone le potenzialità dal punto di vista degli studenti e
dei docenti.
La redazione del sito può essere contattata all'indirizzo: redazione@quadernoaquadretti.it
Più matematica per chi insegna matematica
Maria Dedò, settembre 2001
La domanda a cui mi è stato chiesto di rispondere in questo intervento è una domanda estremamente vasta: quale può essere il significato della ricerca nel campo della didattica della matematica; quale può essere tale significato oggi in Italia, con un occhio a ciò che accade nel mondo e un inquadramento in ciò che è accaduto in passato, prendendo le mosse in particolare da due articoli la cui traduzione in italiano è stata recentemente pubblicata su questa stessa rivista ([1] e [2]).
Potenzialità di un apprendimento informale
Maria Dedò Torino, 10 Aprile 2015 Liceo D'Azeglio
Matematita è un Centro di ricerca che si è costituito nel 2005, raccogliendo esperienze preesistenti che da anniesploravano le potenzialità di strumenti come mostre, libri, kit di laboratorio per le scuole, video, ecc. Punto di partenza: è cruciale il momento dell’apprendimento informale e occorre quindi studiare come ottimizzarlo. La formalizzazione certamente dovrà esserci, ma soltanto dopo che l’apprendimento informale si è consolidato, negli ultimi anni si è ormai riconosciuto in maniera abbastanza unanime l’importanza di una modalità di apprendimento laboratoriale.
SCUOLA PRIMARIA
Torri, serpenti e… geometria Giocare con le forme Effetto domino - giochi di aritmetica (SOLO per la V classe)
SCUOLA SECONDARIA DI I GRADO
Simmetria: matematica in giardino Uguali o diversi Forme. La matematica mette in ordine
Uguali o diversi Nastri. La matematica mette in ordine
Uguali o diversi Stelle. La matematica mette in ordine
Uguali o diversi Tombola! La matematica mette in ordine
Uguali o diversi Domino. La matematica mette in ordine
Il viaggio segreto - giochi di aritmetica (SOLO per la II e la III classe)
Effetto domino - giochi di aritmetica (SOLO per la I classe)
Specchi - osservare la simmetria
Simmetria: dagli specchi alla carta
Diamo forma alla geometria -
regolari o no?
Diamo forma alla geometria -
grande o piccolo?
Come insegnare la Matematica
Intervista a Ana Millan Gasca
Docente di Matematiche complementari presso l'UniTre di Roma. I bambini sono circondati dalla Matematica, dalla pubblicità alla vita quotidiana. Partire dall'esperienza per sviluppare la loro curiosità.
Matematica e studenti italiani: tutto da rifare?
Intervista con Rosetta Zan
Secondo l’ultima indagine OCSE-PISA i quindicenni italiani hanno scarse competenze in Matematica. Come leggere questi dati? Come farli diventare un pungolo positivo per gli ordini inferiori di scuola? Riprendiamo un'intervista con Rosetta Zan, che ha insegnato Didattica della Matematica all’Università di Pisa, apparsa sul sito La Vita Scolastica.
È la terza edizione di MathUp! I corsi si sono tenuti per la prima volta nell’anno scolastico 2015-2016. Il successo delle prime due edizioni è stato incoraggiante (cfr. anche il successivo “I numeri delle precedenti edizioni”) e il progetto dunque continua, tenendo naturalmente conto dell’esperienza acquisita e del desiderio di fare sempre più e meglio.
Ogni docente apporterà nei propri corsi le innovazioni che giudicherà opportune, ma nella sostanza la struttura di MathUp esce confermata dall’esperienza degli anni passati.
Le principali novità della terza edizione sono:
- la riproposizione delle video-lezioni registrate negli a.s. 2015-16 e 2016-2017;
- l’apertura dei corsi dedicati alle classi successive a quelle toccate lo scorso anno, vale a dire la quinta della scuola primaria, la terza della scuola secondaria di I grado, la quinta della scuola secondaria di II grado;
- la particolare attenzione dedicata all’insegnamento della matematica negli Istituti professionali con l'approfondimento del corso rivolto specificamente alla prima classe di tali Istituti;
- la proposta di una community volta a elaborare e proporre specifici percorsi, laboratori, prove di verifica da usare direttamente nelle classi del primo biennio delle superiori (con riferimento alle video-lezioni già realizzate per questo segmento scolastico);
- la possibilità di impiegare i laboratori previsti nella seconda fase dei corsi per l'alternanza scuola-lavoro (cfr. “Come sono organizzati”);
- la modalità di iscrizione “presenta un collega” (cfr. “La quota di iscrizione”).
Che cosa sono; Vorrebbero non essere i soliti corsi di aggiornamento; Chi li organizza; A chi sono rivolti; Le motivazioni; Le parole-chiave; Obiettivo "fare pace con la matematica";
Obiettivo "studenti oggi, professionisti domani"; Come sono organizzati: le due fasi e il rapporto con l'alternanza scuola-lavoro; La prima fase; Docenti e tutor nella prima fase;
Le tappe intermedie; I programmi dei corsi; Gli attestati al termine della prima fase; La seconda fase; I tutor e le collaborazioni nella seconda fase;
Gli attestati al termine della seconda fase; Accreditamento dei corsi MathUp presso il MIUR; I numeri delle precedenti edizioni; a quota di iscrizione; La carta del docente;
Come e quando iscriversi; Contatti; Newsletter; FAQ
Raccogliamo qui le presentazioni delle relazioni e alcuni materiali extra che i relatori ci hanno suggerito come complemento alla loro relazione.
Alcuni amici, per giocare a campana sulla strada, disegnano con il gesso, sul pavimento della piazza del paese, una piramide con i numeri. Ogni numero nei rettangoli rossi è la somma di quelli nei due rettangoli verdi subito sotto; ogni numero nei rettangoli gialli è la somma di quelli nei due rettangoli rossi subito sotto e il numero nel rettangolo blu è ottenuto nello stesso modo a partire da quelli scritti nei due rettangoli gialli. La pioggia, però, ha cancellato alcuni numeri. Sapreste dire che numeri sono? scriveteli ai loro posti.

Tesi di Laurea in didattica della Matematica
di Maria Pezzia, relatore prof. Paolo Guidoni
Questo lavoro rende conto di un intervento di ricerca–azione realizzato in due prime elementari durante l’intero anno scolastico 2003/2004. Tale intervento costituisce la prima tappa di un progetto di sperimentazione didattica che sarà portato avanti nelle due classi fino alla quinta, e che ha come oggetto la trasmissione e l’acquisizione delle strutture elementari dell’aritmetica: durante questo primo anno si è lavorato fondamentalmente sul “significato del contare”, individuato attraverso i suoi legami con la struttura additiva (somma e sottrazione) e con la struttura moltiplicativa.
L’obbiettivo della ricerca è stato quello di costruire e, insieme, mettere alla prova un possibile “modello” di intervento didattico: siamo partiti da alcune attività già sperimentate in altri contesti di ricerca (in particolare il Progetto MIUR ‘97-’99 “Capire si può”) e abbiamo provato ad applicarle adattandole alla situazione da noi scelta, modificandole in corso d’opera e integrandole con nuove idee per rispondere alle esigenze di comprensione e alle difficoltà emerse lavorando con i bambini. (170 pagine con introduzione, finalità, esempi didattici...)
Progetto didattico: “La ballata degli elefanti”
Attività programmate:
1. Gioco “Regina reginella” (passi degli animali: formica, elefante, gatto, uccellino, pulcino, coccinella....)
2. Gioco “ Avanti e indietro”: 1° tutti su una riga, 2° ognuno in posizionediversa.
3. Ascolto e ballo libero della canzone “La ballata degli elefanti”
4. Gioco: ognuno decide da dove partire si segna con lo scoch e poi esegue i passi avanti e indietro segnandoli (ogni passo avanti con un tappo rosa, ogni passo indietro con un tappo bianco). Si decide come fare lunghi i passi e se usare come unità di misura la mattonella.
5. Provare e riprovare finchè tutti non sono padroni della linea dei numeri: sopra e sotto lo zero. Notare le difficoltà.
Commento “matematico” a “La ballata degli elefanti”
Paolo Guidoni
<E' la ballata – degli elefanti – tre passi indietro – due passi avanti …>Per un avvio al gioco vedere il corrispondente capitolo della tesi di Maria Pezzia, che documenta quello che è successo in una delle (tante) situazioni in cui il gioco è stato utilizzato.Il commento che segue non è una “ricetta per come giocare”: un gioco-prototipo (come questo, e altri) “serve” se è giocato (in quanto è giocato) in maniera aperta (e progressiva) rispetto alle infinite variazioni/elaborazioni possibili – sia da parte degli adulti che dei bambini.Questo commento è ad uso degli adulti che, dopo aver avviato il gioco e motivato i suoi primi sviluppi, vogliano vedere un po’ più in chiaro <dove si può andare a finire> - dal solo punto di vista di un percorso di progressiva appropriazione del <senso del numero> da parte dei bambini. (Sempre tenendo presente che si tratta soltanto di un punto di vista parziale, rispetto alla validità globale del gioco stesso)...
La storia di Martina e il Gigante
Paolo Guidoni
Premessa
La storia, come sempre, deve essere aggiustata-arricchita-semplificata-variata-continuata-ripresa-complicata … secondo la situazione: con la collaborazione dei bambini, una volta avviato il gioco, se si vuole che serva (insieme a tante altre!) per l’appropriazione di strategie generali adatte a “mettere in ordine” il mondo; e comunque senza “forzare” automatizzazioni che poi servono a poco, se non derivano da un uso che corrisponda a una varietà di scopi e significati, e da un apprezzamento “meta cognitivo” della loro efficacia.
La storia è solo accennata schematicamente – ma anche così diventa, al solito, troppo lunga da scrivere “per bene”: è importante sviluppare come Insegnanti una naturalezza (anche) di “canta- storie-finalizzate” da scambiarsi reciprocamente – messe magari in forma “minimale” - attraverso cui condividere e utilizzare le molte idee che vengono lavorando con i bambini senza dover appesantire troppo la comunicazione con “storie-proprio-così”
Ovviamente fa parte essenziale dell’attività sia la ri-proposta individuale/collettiva della storia da parte dei bambini, anche senza una vera e propria drammatizzazione accurata – comunque sempre molto efficace; sia l’attività centrata sul ri-rappresentare subito dopo con un “disegno promemoria” quello che è successo maneggiando oggetti: cogliendo, gradualmente e per approssimazioni successive, il significato e soprattutto il senso delle diverse schematizzazioni- simbolizzazioni coinvolte. [leggi tutto]
Il pastore Gioele ha un piccolo gregge con 40 pecore e il cane Melampo, e deve attraversare il fiume.
Il barcaiolo Ascanio ha una piccola barca che può portare al massimo una persona e 8 pecore, oppure due persone e 6 pecore. (Un cane occupa il posto di una pecora).
Per ogni viaggio (andata e ritorno) Ascanio chiede un compenso di 4 euro.
Nel primo viaggio bisogna che in barca ci sia anche Melampo, che poi rimane a fare la guardia alle pecore di là dal fiume.
Nell’ultimo viaggio bisogna che in barca ci sia anche Gioele, che è rimasto per far salire tutte le pecore.
Quanto spende Gioele?
La bella Kadija dagli occhi blu [versione completa con immagini .pdf]
Acqua, colore e pensiero proporzionale
Proposta di contesti significativi per estendere la gamma dei riferimenti per i sensi del concetto di proporzionalità e favorirne la generalizzazione.
Classi coinvolte
La proposta è rivolta alla classe V^ della scuola primaria e alle classi I^ A e I^ B
della scuola secondaria di primo grado.
Docenti
Scuola primaria
Casati Vera (italiano, arte e immagine), Vignali Claudia (matematica, scienze e tecnologia) Menciassi Rossana (sostegno)
Scuola secondaria di primo grado
Fantoni Sara (matematica e scienze), Testi Maura (matematica e scienze), Ferri Arianna (italiano), Montagnani Michela (italiano) (...)
La narrazione
Tanto tempo fa in un palazzo dell’India viveva una bellissima fanciulla che si chiamava Cadija ed era la figlia del sultano.
La parte particolare dell’aspetto fisico di Cadigia erano i suoi occhi; che erano di un colore azzurrognolo sfumato di un celeste chiaro.
Un giorno Cadigia si affacciò alla finestra del palazzo del padre.
Lì vicino stava passando un uomo di nome Amos ed era ricco, prepotente e crudele ed era accompagnato dalle sue guardie del corpo; guardò verso la finestra di Cadigia; lui si innamorò immediatamente di lei e decise di chiedere al sultano la mano di sua figlia.
rete galileo – gruppo di sperimentazione
Non solo far di conto [versione completa .pdf]
percorsi integrati di matematica e scienze nella scuola di base
Benevento 2010
Questo volume è stato prodotto grazie al finanziamento PON Progetto B1-FSE-2009-926
Contributi di
Brunella Brillante, Stefano Califano, Orsola Ciarlo, Ester Cocchiarella, Giulio De Cunto, Mariateresa De Pietro, Filomena Di Biase, Angelina Di Santo, Rosa Ferrara, Angela Follo, Michelino Frattolillo, Antonietta Guerra, Rossana Guerra, Paolo Guidoni, Donatella Iannece, Anna Maio, Gina Marino, Ciro Minichini, Carmela Pagnozzi, Antonietta Palma, Patrizia Parlapiano, Maria Maddalena Pascarella, Concetta Maria Torrillo, Roberto Tortora, Maria Giuseppa Vallarelli, Michelina Venditto, Roberta Virgilio.
Indice
Presentazione 5
Introduzione
Cambiare si può: per esempio 9
Capitolo I
Sommare numeri consecutivi 19
Capitolo II
Prime Forze: schemi per guidare l’inizio
di un percorso di comprensione 61
Capitolo III
Galleggiamento 89
Capitolo IV
Acqua e zucchero: una “dolce” situazione
problematica 127
Appendice
Accordo di Rete “Galileo” 171
Esempi schematici di percorsi-prototipo
Percorso-i: rapporto e proporzione in situazioni di fittezza [scarica .pdf]
Paolo Guidoni
I.1) Una digressione preliminare e schematica su rapporto e proporzione
La ricerca (con bambini e adulti) mostra che ci sono diverse “famiglie” di situazioni di esperienza che sono intuitivamente viste come caratterizzabili da un rapporto: ma che, in origine, sono considerate diverse fra loro sia nel significato sotteso che nei riferimenti percettivo-motori, e quindi incontrano difficoltà ad essere ricondotte a un unico modo di vedere e di ragionare – quindi a un unico “formalismo”.
In particolare, per esempio:
I.1a) Contesti di azione ripetuta, analizzati in termini di tre variabili percettivamente evidenti e di differente significato [cose(c) - volte(v) - cose alla volta(c/v)], in genere “diacronici” in quanto coinvolti in uno svolgimento temporale progressivo (implicito nella parola <volte>, eventualmente preorganizzato rispetto all’azione): contesti che sboccano nelle tipologie standard di “divisione di ripartizione” e/o “divisione di contenenza”, e hanno come “figura” complessiva caratterizzante lo “schieramento” (schema “sincronico”, da cui peraltro risultano evidenti tutte le proprietà delle operazioni di moltiplicazione e divisione, incluse le relazioni fra semantiche di contenenza e di ripartizione, i rapporti non interi, etc).
Laboratorio: La calcolatrice ed il “far di conto”
Alessandra Gamba
Insegnante di scuola primaria
Istituto Comprensivo San Biagio di Callalta
L’uso della calcolatrice in classe incontra molte resistenze da parte di ge- nitori e insegnanti perché viene interpretato spesso solo come una facilita- zione di calcoli. In realtà questo strumento può dare un supporto alla co- noscenza del nostro sistema di numerazione, alle proprietà delle operazio- ni ed il ruolo di protagonista che riveste può aiutare a superare i pregiudizi di genitori ed insegnanti.
Mimma Liber
In una conferenza il prof Giacomo Stella[1] individuava una delle debolezze strutturali della scuola italiana nella mancata coerenza delle più diffuse strategie scolastiche con i reali processi di apprendimento degli allievi; la prassi corrente, specie nelle scuole superiori, è quella della lezione frontale, seguita da esercitazioni e conclusa dalle prove di verifica. Una procedura che non tiene conto dei diversi stili cognitivi, delle spesso mancate motivazioni degli studenti, dello sforzo di comprendere informazioni e di sistemarle in sintesi coerenti e significative: l’insegnamento e l’apprendimento così spesso si appiattiscono, riducendo i contenuti disciplinari a frammenti di conoscenza da ritenere e memorizzare a scadenza medio-breve per superare le interrogazioni e i compiti in classe. Eppure i processi conoscitivi sono stati ampiamente esplorati dalla pedagogia più recente: essi dovrebbero far parte della cultura professionale degli insegnanti, che arricchirebbero così il proprio bagaglio di strategie didattiche nell’insegnamento dei saperi disciplinari.
Il CIDIS, esplorando queste tematiche, ha proposto ai docenti nel 2015 un corso di formazione dal titolo Homo ludens, con la scommessa di ritrovare nelle dinamiche del gioco le “mosse vincenti” di un apprendimento nello stesso tempo stimolante e significativo. Ne sono nate proposte accattivanti su più discipline, fra le quali italiano, storia, matematica e scienze: proposte che hanno messo in luce la struttura profonda dei saperi, proprio perchè si è cercato di fondare gli stimoli da proporre agli allievi sullo statuto epistemologico delle discipline affrontate.
Provo qui ad accennare a come ho interpretato l’allievo ludens in matematica. [continua a leggere] [presentazione]










