Dal soppesamento al galleggiamento:
esperienze di peso / massa / volume, grandezze in relazione
Laura Moreni, Maria Castelli quarta e quinta classe, 2007-2008
Abbiamo colto come un’opportunità da non perdere l’elaborazione della tesi di laurea di una delle autrici (L.M.) nella classe dell’altra (M.C.) per svolgere un percorso fra matematica e scienze, con il supporto di una docente universitaria esperta in didattica della matematica (*). Il tema proposto era stato la misura, con particolare riferimento ai concetti di peso e di massa, che rappresenta un filo conduttore lungo e ricorsivo, che si dipana dalla prima classe fino all’ultima in matematica e costituisce la struttura della conoscenza scientifica. Contando sulla supervisione di un’esperta disciplinare ed avendo negli anni scorsi già provato alcune attività, ci siamo sentite di correre il rischio di affrontare concetti solitamente ritenuti difficili per bambini di questa età, con l’obiettivo di verificare se essi fossero proponibili con un approccio prevalentemente laboratoriale. Anche per questo motivo, dopo una progettazione iniziale a maglie larghe, abbiamo proceduto passo passo, attente sempre alle restituzioni dei bambini, prima di definire la proposta successiva. Il lavoro è incominciato in quarta classe con la tesi e proseguito in quinta per dare una momentanea conclusione ai temi aperti, coinvolgendo i 43 bambini di due classi per poco più di sei mesi, per due ore alla settimana per ciascuna classe.
Nel presidio ISS di Brescia, abbiamo condiviso e discusso con i tutor, uno dei quali è un’insegnante di fisica e con altre colleghe la progettazione e la realizzazione delle attività, che sono state in parte inserite anche nei percorsi di apprendimento di altre classi.
Elementi concettuali ed operativi essenziali
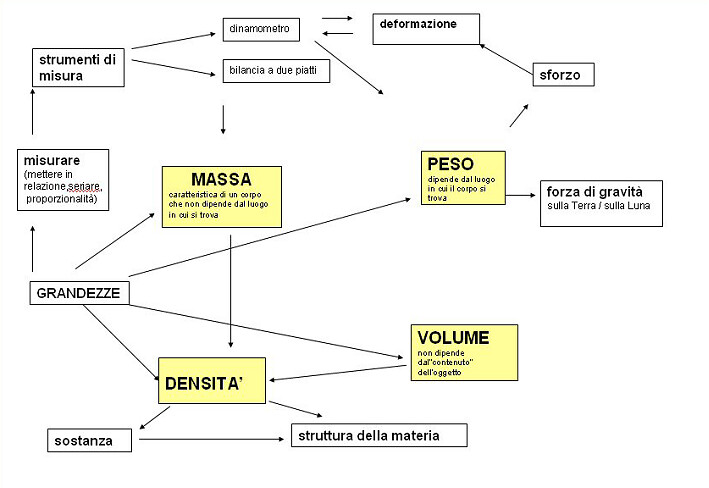
In fase di prima progettazione, la nostra attenzione è sui concetti disciplinari di matematica e di scienze in gioco e sulle abilità che gli alunni potranno esercitare nei contesti laboratoriali che si andranno a creare. (fig. 1)
Si tratta dell’idea di grandezza da maturare attraverso l’operatività richiesta dalla misurazione: si partirà dal peso – dalle conoscenze spontanee elaborate dai bambini nei loro vissuti, in una consuetudine che confonde i significati – poi si rifletterà sugli “effetti” della pesantezza degli oggetti quali la caduta, lo sforzo e la deformazione per arrivare, dopo aver conosciuto il filo a piombo ed aver ragionato su che cos’è verticale / orizzontale, alla costruzione di uno strumento adatto a misurare il peso.
La narrazione e il documentario NASA dello sbarco sulla Luna introdurranno alla seconda grandezza, la massa, che, a differenza del peso, potrà essere colta come caratteristica di un corpo indipendente dal luogo e misurata con la bilancia a due piatti.
Il volume degli oggetti è la grandezza che può presentare meno difficoltà, anche se occorre trovare strategie praticabili per la misurazione.
A questo punto bisogna vedere come variabili le grandezze appena conosciute, per studiare operativamente e rappresentare come cambiano l’una rispetto all’altra: l’idea di densità dei diversi materiali utilizzati si farà strada nella mente dei bambini come “più o meno pieno”, “più o meno fitto”, “più o meno concentrato”, portando a maturare un primo modello di struttura della materia e facendo luce sulla possibilità di galleggiare nell’acqua o in altre sostanze.
Alcune situazioni incontrate o intenzionalmente create sono il pretesto per affrontare / riprendere concetti propriamente matematici quali le relazioni logiche, la proporzionalità e la sua rappresentazione nel piano cartesiano, “perpendicolare” come parola del lessico geometrico anziché “verticale / orizzontale” come parole che descrivono il mondo fisico, le unità di misura di massa, di peso e di capacità/volume.
Il percorso in classe
1- Il peso: dal recupero dell’esperienza dei bambini alla misurazione
Per dare avvio al percorso era necessario indagare ciò che i bambini già conoscevano rispetto al peso. A quest’età, il modo che meglio permette l’analisi delle conoscenze pregresse è la conversazione, intesa come ascolto dei pensieri e delle convinzioni della classe, senza interferire nelle risposte. Dopo aver ricordato le discussioni di terza sugli attributi misurabili degli oggetti e gli snodi cruciali dei ragionamenti sulla misurazione delle lunghezze e della capacità già svolti, si è chiesto che cosa sapessero del peso e come si potesse misurare. Ecco alcune risposte, nelle quali si evidenziano alcune conoscenze dei bambini da tenere in considerazione per la progettazione:
Mc.- Un oggetto può essere pesante o leggero.
G.- Si può misurare con la bilancia.
Gr.- Io non so bene cosa sono però ho sentito che qualcosa si chiama tara, peso netto, e poi ce n’è un altro …
C.- Il peso è la forza della gravità che tira l’oggetto, l’uomo o l’animale verso il centro, solo che non lo porta proprio giù perché c’è la terra che copre, poi c’è la sfera di fuoco e così non ci si brucia.
Gg.- Anche il peso ha dei campioni come il chilogrammo, il grammo, l’etto …
F.- Il peso di un oggetto varia dalla grandezza: se un oggetto è grande pesa di più, se un oggetto è piccolo pesa di meno.
V.- A parte le cose piccole, come il capello.
V.- Pesano anche quelle piccole, ma di meno.
C.- Un oggetto pesa di più se è pieno, se è vuoto, se non ha aria o acqua, pesa di meno.
St.- Se è vuoto ha dentro l’aria.
St.- Se però prendi un polistirolo che è grande e un piombino che è piccolo, pesa più il piombino del polistirolo.
Ma.- I sassi sono piccoli ma pesano.
Gi.- Se la busta dei compiti è vuota pesa poco, se è piena pesa di più.
Gg.- Ci sono cose senza peso: per esempio l’aria, i nei, i punti sulla faccia, un pezzetto di carta piccolissimo.
Gr.- A proposito di quello che ha detto Gg., primo l’aria pesa, ci sono anche delle cose astratte, come l’anima che secondo me non pesa…
Gg.- I sentimenti pesano, dipende da quanti ne hai, come per esempio l’amore, non è che pesano, ma pesano nei nostri riguardi.
Si.- Le cose astratte non pesano.
G.- Però ci sono sentimenti che in un certo senso ti pesano, se uno si lascia, per esempio, all’altro pesa, si sente non bene, sta male.
………..
Come si fa a misurare il peso di un oggetto?
St.- Usi la bilancia.
St.- Lo confronti con un altro oggetto che pesa più o meno, li prendi in mano tutti e due e poi li confronti, uno per ogni mano.
Gg.- Faccio il confronto diretto, uno per mano.
F.- Cerchiamo la differenza.
Sil. e El.- Facciamo una previsione, una stima.
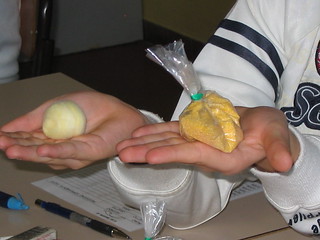
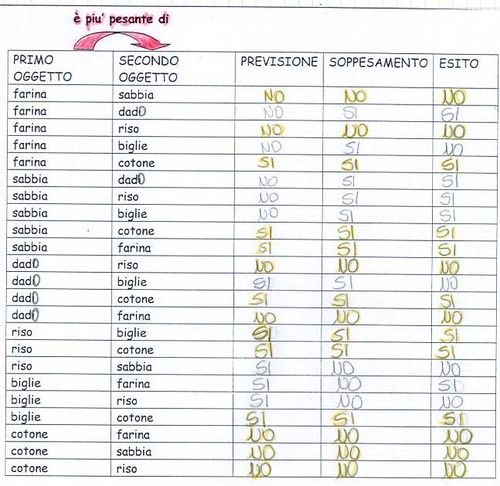
Ai bambini si è proposta una breve attività di confronto diretto qualitativo ad occhio di alcuni oggetti presenti in aula, chiedendo di osservarli, di prevederne il peso e di ordinarli dal meno pesante al più pesante. Ha fatto seguito la prima verifica mediante il soppesamento con le mani. (fig.2) Sono sorti alcuni dubbi: non si poteva essere certi che la seriazione fosse corretta, perché quanto percepito con le mani può essere errato, non oggettivo. I bambini, allora, hanno proposto di controllare mediante uno strumento: la bilancia. In seguito si presenta un’ulteriore attività di soppesamento più strutturata, con oggetti appositamente predisposti. In una tabella a doppia entrata erano elencate le coppie di oggetti da porre a confronto; dapprima si è richiesto di formulare previsioni, poi di verificare con l’utilizzo della bilancia a due bracci per costruire la serie dal più pesante al meno pesante. (fig. 3)
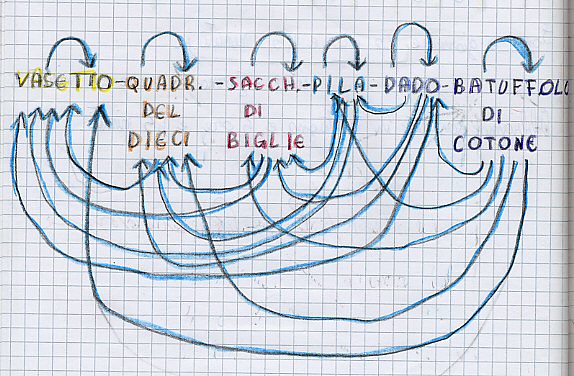
La tabella utilizzata per la registrazione dei soppesamenti era stata predisposta proponendo alcune coppie in cui l’ordine degli oggetti si presentava semplicemente invertito: è stato questo lo spunto introdotto per esplorare le relazioni logico-matematiche, analizzandone e riscoprendone le proprietà riflessiva, simmetrica e transitiva. La fig.4, è un esempio di rappresentazione con diagrammi sagittali di un’attività sulla relazione ”io non sono più pesante di te”.
 |
 |
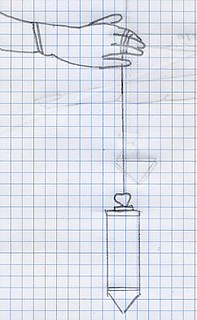
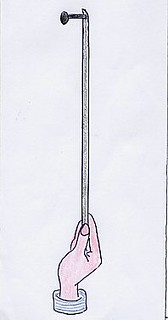
Dopo questo approfondimento matematico, affrontato con molti esempi in situazioni diverse, si è ritornati al peso mediante la presentazione del filo a piombo, che i bambini hanno utilizzato e disegnato. I lavori prodotti hanno dato luogo a due diverse rappresentazioni: una che metteva in evidenza correttamente la tensione del filo dovuta al peso del piombo e l’altra che non ne teneva conto.(fig.5 a, b)
Una breve conversazione ha permesso di evidenziare che in fondo al filo c’è un oggetto pesante che lo tende rendendolo verticale.
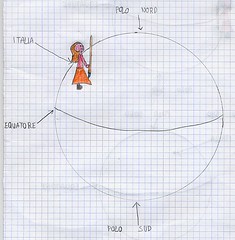
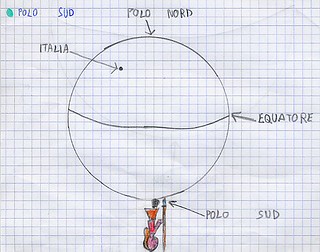
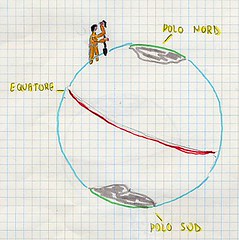
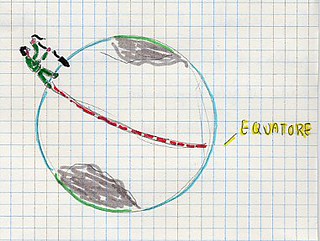
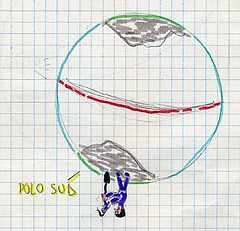
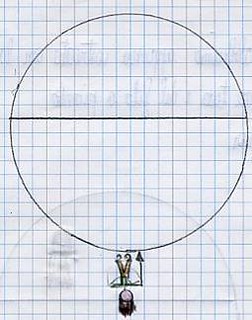
Sul concetto di verticalità si sono sviluppate le lezioni successive, con l’obiettivo di condurre la classe a riscoprirlo inteso come direzione della forza peso. Si è trattato di un passaggio delicato e non facile dell’itinerario didattico che ha segnato l’avvio di una presa di consapevolezza della distinzione tra spazio fisico e spazio geometrico. Si è proceduto utilizzando alcuni modelli materiali caratterizzati da un progressivo livello di astrazione: incominciando dalla lettura del globo terrestre, che viene in seguito sostituito con una grande palla sulla quale si tracciano i poli, l’equatore, la posizione dell’Italia, si è poi discusso e ragionato con l’aiuto di un omino con un’asticciola in mano per rappresentare il filo a piombo.
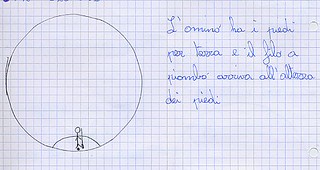
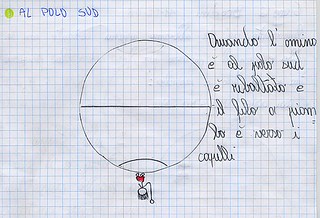
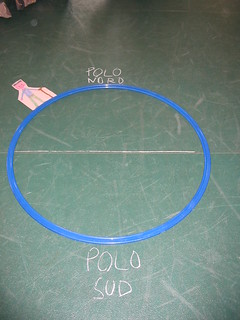
Un passaggio successivo ha richiesto di rappresentare da soli quanto osservato. I disegni sono stati raggruppati secondo le diverse categorie di errori (fig.6) e discussi, anche con l’aiuto di altre modellizzazioni in palestra (fig. 7 a, b, c) per giungere a riscoprire che il filo a piombo ha una direzione verticale che è perpendicolare alla superficie terrestre, la quale ha una direzione definita orizzontale.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
L’utilizzo di alcuni termini, come perpendicolare, ha permesso un approfondimento relativo al fatto che nello spazio geometrico non sia possibile parlare di verticale / orizzontale, poiché entrambi i concetti si definiscono nello spazio fisico, nel quale la forza di gravità dà ad essi significato.
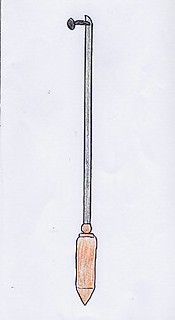
L’attenzione è stata posta poi sul tipo di filo che sostiene il piombo. La distinzione lessicale tra elasticità, flessibilità e plasticità ha permesso di notare che il sostegno del filo a piombo fosse flessibile, non elastico. Abbiamo valutato gli effetti che, prima la forza di una mano e poi corpi pesanti, producevano su diversi tipi di elastici; infine i bambini, dopo aver formulato previsioni sull’allungamento causato dagli oggetti già usati nel soppesamento iniziale, le hanno verificate con una sorta di dinamometro artigianale, senza alcuna scala metrica: si è ottenuta una seriazione dall’oggetto che allunga di più a quello che allunga di meno identica a quella ottenuta con i soppesamenti iniziali. Ciò ha consentito di formulare una prima importante conclusione: soppesando gli oggetti con le mani e osservando l’allungamento di un elastico si verifica il peso degli oggetti in due modi diversi.
Dopo la rilevazione qualitativa, è stata indagata la causa dell’allungamento dell’elastico mettendo in gioco il concetto di forza, nella sua specificazione di peso / forza di gravità.
Ponendo a confronto le schematizzazioni delle diverse situazioni di allungamento precedentemente sperimentate (fig.8 a, b, c), i bambini hanno indicato come causa comune l’applicazione di una “forza” in un caso esercitata dal braccio, negli altri due dalla Terra che “richiama” l’oggetto verso il basso, verso di sé; abbiamo chiamato peso questa forza e siamo giunti ad una seconda conclusione: la forza che tira verso terra è la forza di gravità ed è il peso del corpo.
 |
 |
 |
Quarta A
L. – Sono forze diverse.
N. – La forza dei muscoli è quella che tira di più.
M. C. – Due sono pesi, la prima è una forza.
J. – Non è detto che la forza dei muscoli tiri sempre di più…se è un bambino piccolo a tirare…
L. – Forza e peso, tutte e due tirano in giù.
C.– Con la forza dei muscoli puoi tirare in tutte le direzioni, il peso tira solo in giù, in verticale verso terra.
N. – Con la forza dei muscoli puoi tirare di più o di meno, con il peso c’è un limite, quello del peso dell’oggetto, di più non si può.
Quarta B
S. – E’ come se a tutti gli oggetti ci fosse un filo attaccato alla forza di gravità e la forza di gravità è il peso.
F. – Senza la forza di gravità, niente avrebbe peso.
G. – Se non ci fosse la forza di gravità, allora una persona non peserebbe?
M.– La persona avrebbe il suo peso, ma non lo sentirebbe senza la forza di gravità.
Questo intervento sarà prezioso quando, dopo la narrazione “Martino su Marte” e dopo il documentario degli astronauti sulla Luna, si arriverà alla dissonanza che ci permetterà una prima distinzione fra peso e massa.
G. G. – D’accordo!
V. – Io non riesco a sollevare cose molto pesanti, ma se non ci fosse la forza di gravità riuscirei.
L. – Senza forza di gravità la scuola volerebbe?... Ma ha le fondamenta…
Conclusa l’analisi e la discriminazione qualitativa delle grandezze, è stata affrontata la questione della quantificazione del peso, utilizzando un dinamometro artigianale: il problema proposto era di determinare la relazione tra l’allungamento dell’elastico e il numero di “oggetti unitari” appesi, nel caso specifico biglie. Nelle prove condotte raddoppiando, dimezzando e triplicando l’iniziale numero di biglie, i bambini hanno riconosciuto la relazione di proporzionalità diretta tra il numero delle biglie e l’allungamento dell’elastico, nel rispetto della massima tollerabilità e della sensibilità dell’elastico stesso. Scegliendo come peso unitario quello del sacchetto con tre biglie, abbiamo tarato il dinamometro artigianale ed effettuato misure ed equivalenze (fig. 9 a, b, c).
 |
 |
 |
A questo punto, sono stati forniti ai bambini alcuni dinamometri con i quali hanno provato a pesare gli oggetti utilizzando l’unità di misura del peso, il newton (fig.10 a,b,c).
 |
 |
 |
2 -La massa: la narrazione e le immagini, suggestioni per far emergere dissonanze cognitive
Per accompagnare il percorso, nel modo di uno sfondo integratore, da settimane, leggo alle classi il libro “Martino su Marte” (1), che risulta coinvolgente per tutti i bambini grazie alla sapiente amalgama di simpatia dei protagonisti, narrazione fantasiosa e curiosità delle informazioni scientifiche.
Vediamo insieme il filmato dello sbarco sulla Luna (2) e, una volta ritornati in classe, sottolineo alcuni aspetti evidenziati nel filmato con la lettura di alcune pagine del testo di narrativa citato.
Poi si discute. Che cosa vi ha colpito del filmato?
G. – Il razzo, la partenza! Faceva paura. E la Luna con tutte le buche che è diversa da come la vedi da qui.
F. e A. – Li vedi anche da qui i crateri.
C. – Quando sono andati in bagno gli astronauti…
V. – Le dimensioni del razzo.
M. – La Terra dall’alto.
I. – Noi vediamo il cielo azzurro, nello spazio è nero, perché?
F. – E’ l’aria, è l’atmosfera…
Ne riparleremo….
G. Ghi – Gli oggetti che galleggiavano nella navicella, poi la Luna mezza chiara e mezza scura…
Che cosa facevano di diverso gli astronauti?
M. – Saltellavano perché c’è poca forza di gravità.
M. Chi – Secondo me c’è un po’ di forza di gravità perché se non ci fosse, gli astronauti saltando resterebbero in aria.
C. – C’è la forza di gravità perché piuma e martello sono caduti, sennò come facevano?
Tutti sono d’accordo: sulla Luna c’è poca forza di gravità ma c’è; è stato detto nel filmato e lo dice anche Martino…….
Se gli astronauti diventano più leggeri, che cosa succede al loro peso?
In B, tutti dicono che il peso è sempre uguale; ti senti più leggero, ma sei sempre tu.
In A, 12 sostengono che il peso resta lo stesso; 6 che si pesa meno sulla Luna, 3 pensano che si pesi di più sulla Luna.
Propongo la seguente intervista all’astronauta Umberto Guidoni:
Che cosa si prova in assenza di gravità?
Si parla di assenza di peso e non di assenza di gravità, che invece è sempre presente ed è la forza che fa compiere alla navicella la sua orbita. Me la posso cavare con una battuta, si sta “leggeri”, ma una risposta vera è più complicata. C’è un periodo di adattamento, che può durare poche ore o qualche giorno, di cui il nostro corpo ha bisogno per orientarsi nella nuova condizione in cui non c’è più alto e basso. In una situazione in cui muoversi non richiede alcuna fatica, il cervello ed i muscoli devono imparare a coordinarsi. Quindi, all’inizio, ci si sente come un pesce fuor d’acqua, poi si “impara a nuotare” ed ho usato questo verbo non a caso perchè essere in assenza di peso assomiglia molto a trovarsi immerso nell’acqua, la stessa sensazione di galleggiamento ma senza l’acqua!
Che cosa fai nella navicella quando non devi lavorare?
La mia attività preferita nelle rare pause, che possiamo chiamare “tempo libero”, durante la permanenza sulla Stazione Spaziale Internazionale era guardare la Terra e l’immagine che mi è rimasta più impressa è ovviamente quella dell’Italia: un ponte sul Mediterraneo tra Europa ed Africa.
Com’è la vita quotidiana a bordo? Come si mangia, come ci si lava e come si dorme?
L’attività di bordo è pianificata nei dettagli e si segue alla lettera quello che viene chiamato “piano di volo”. Normalmente si lavora per 12 ore, con un periodo di sonno di 8 ore e le restanti quattro ore, due prima e due dopo il periodo di riposo, vengono utilizzate per le attività personali. Anche se si ha una giornata simile a quella terrestre, il continuo cambio tra luce e buio crea una sfasatura che finisce per aumentare la stanchezza alla fine della giornata di lavoro. Anche per le attività più comuni come mangiare, dormire o fare sport ci si trova a fare i conti con l’assenza di peso, che rende tutto molto più difficile. Non ci può essere acqua corrente e ci si lava con sapone senza schiuma che si toglie con panni umidi; per mangiare bisogna utilizzare dei contenitori di plastica, che contengono cibi precotti e disidrati, altrettanto per le bevande che si sorseggiano con la “cannuccia”. Per dormire si usano dei sacchi a pelo stesi fra il soffitto d il pavimento: nello spazio si dorme “in piedi”!
L’uomo un giorno potrà andare a vivere sulla Luna?
Per la Luna, la Nasa è già impegnata nella preparazione di missioni di esplorazione umana alla fine del prossimo decennio. Tra 30-40 anni comincerà l’esplorazione di Marte ed entro il prossimo secolo, sarà possibile stabilire colonie umane autosufficienti. Da lì, ci si potrà spingere verso la periferia del nostro Sistema Solare ed esplorare i satelliti di Giove, alcuni dei quali, come Europa, con distese di ghiaccio che ricoprono oceani di acqua dove potrebbe essersi sviluppate forme di vita aliene. Forse qualche centinaio di anni saranno sufficienti per sviluppare le tecnologie che ci permetteranno di costruire piccoli pianeti artificiali autosufficienti, delle vere e proprie “oasi abitate” in grado di navigare per moltissimo tempo negli abissi cosmici, portando con sé una comunità in evoluzione, pronta ad istallarsi su altri pianeti abitabili.
La visione del documentario, la lettura del libro e l’intervista hanno aiutato a rendere esplicita e più chiara una dissonanza cognitiva. E’ in gioco infatti l’intuizione della distinzione tra i concetti di peso e di massa: osservando i movimenti degli astronauti sulla superficie lunare, i bambini si sono chiesti se lassù diventassero più leggeri, se succedeva qualcosa al loro peso, come se lungo il viaggio avessero perso qualche parte del loro corpo. Se una persona grassa va sulla Luna, là dimagrisce? (Fig. 11)
Passo passo, i bambini hanno intuito che sono due le “qualità” in gioco, non una sola, non solo il peso, ma anche una nuova qualità che si chiama massa: il primo andando sulla Luna cambia, la seconda rimane costante per ciascun oggetto. Sulla Luna si è più leggeri anche se non si dimagrisce (ossia non si perde parte della propria materia): è il peso a cambiare, mentre la massa, cioè la quantità di materia che costituisce un corpo, rimane inalterata. La Luna, più piccola della Terra, trattiene i corpi con una forza di gravità meno intensa, ed essi hanno quindi un peso minore.
Come misurare la massa?
Abbiamo ripercorso tutte le tappe necessarie per misurare una grandezza, tappe già scandite per le lunghezze e per la capacità e ritrovate anche nella taratura della bilancia ad elastico: il confronto diretto prima, quello indiretto poi.
Abbiamo quindi proceduto al confronto diretto della massa di due oggetti mediante la bilancia a due piatti, che ha permesso di rilevare quello che “massa” di più.
E per il confronto indiretto e la quantificazione?
I bambini conoscevano già il nome di qualche multiplo e sottomultiplo del chilogrammo: dopo aver provato a confrontare alcuni oggetti con i pesi-campione contenuti nella pesiera della bilancia, abbiamo costruito la scala delle unità di misura, come già era stato fatto per lunghezza e capacità. Questa è stata l’occasione anche per parlare ai bambini del Sistema Internazionale delle unità di misura e per richiamare alcune regole di scrittura.
3 -Grandezze in relazione: dal volume e dalla massa alla densità
Si è ripreso il discorso in quinta classe, con una breve conversazione finalizzata a cogliere, dopo alcuni mesi, ciò che è più vivamente rimasto ai ragazzi, perché particolarmente gradito / interessante / stimolante, oppure difficile / faticoso. Si è ripercorso passo passo il lavoro di quarta per consolidare quanto appreso, poi si è incominciato a mettere a fuoco una nuova grandezza: il volume. Anche qui, ricordando le esperienze svolte negli anni precedenti, anche con il supporto delle fotografie scattate allora (fig.12 a, b,- fig.13 a, b):
 |
 |
 |
 |
Troviamo tutti i significati di questa parola: un grosso libro, quanto è forte una voce o una musica,……
R. – E’ qualcosa che ingrandisce o rimpicciolisce per lo stesso oggetto, è come la neve che contiene tanta aria e ha un volume più grande dell’acqua che si ottiene con la fusione.
M. – E’ lo spazio occupato da un oggetto.
G. – La quantità (quanto pesa) può essere la stessa, lo spazio occupato può essere diverso, come il bicchiere di neve e l’acqua (di fusione).
P. – E’ come un chilo di paglia che ha un volume grande e un chilo di ferro che ha un piccolo volume.
C. – Un palloncino gonfio ha un volume grande, un palloncino sgonfio ha un volume piccolo…. Qualcuno fotograferà l’impasto di una pizza o di una torta prima e dopo la lievitazione….
Era il momento di cercare una strategia per misurare il volume degli oggetti. Il confronto diretto per ordinare dall’oggetto con volume minore a quello con volume maggiore non ha posto problemi quando le dimensioni erano molto diverse, ma come fare se il confronto diretto non era possibile? Come esprimere con un numero ed un campione anche questa grandezza, come tutti sapevano già fare con la lunghezza, il tempo, la massa, il peso, (e la capacità dei recipienti, per il momento non ancora riconosciuta come volume interno)?
Si è discusso a brevi riprese per diversi giorni. Occorreva anche distinguere che cos’è calcolare e che cos’è misurare. Bisognava trovare una modalità alla nostra portata, ripensando il lungo ragionamento compiuto per le altre grandezze. Infatti da lì i ragazzi sono partiti.
S. e M. C. – Devi riempire l’oggetto con tanti campioni più piccoli…..
Occorre dare qualche indicazione…”cercate idee in quello che fate tutti i giorni”.
M., A., S. – Quando facciamo il bagno! Quando entri nell’acqua è come se l’acqua aumentasse perché tu occupi spazio dentro la vasca.
Si riprende la discussione qualche giorno dopo.
Chi ha fatto il bagno? Chiedo e molti alzano la mano…Ci avete ripensato?
M. – Io non ci ho pensato granchè, ho solo visto l’acqua che si alza di livello.
G. – Entrando io schiaccio l’acqua e lei si alza, l’acqua è sempre la stessa e tanta uguale.
G.G.. – Ho pensato che potremmo fare così a misurare il volume degli oggetti: prendiamo una bacinella, mettiamo un po’ d’acqua, segniamo il livello, mettiamo l’oggetto e il livello sale, segno il livello nuovo, misuro la differenza che è quanta acqua si è spostata.
V. – E’ come quando cammino e l’aria va dove prima ero io, come diceva Alin…..
C. – Possiamo prendere un recipiente, fare tante tacche e guardare quanto sale il livello mettendo dentro l’oggetto.
Così, prima misurando l’acqua tracimata e poi misurando solo il dislivello indicato su recipienti graduati, si è misurato il volume prima in litri e poi in cm cubi, dopo la verifica delle equivalenze.
A questo punto si potevano mettere in gioco due grandezze: il volume e la massa.
Quando aumenta il volume, che cosa succede alla massa ?
G. – Dipende…..
S. – Dipende, perché magari un oggetto di piccolo volume è pieno e ha una massa maggiore di uno che ha un volume più grande ma è vuoto.
M. C. – Può dipendere dal materiale. Il piombo pesa tanto se anche ne prendi una pallina con volume piccolo.
M. De – Se abbiamo i frutti, dipende da che frutto è.
G. – Volevo dire che se un oggetto è grande di volume, ma non contiene niente, cioè solo aria oppure delle piume, avrà una massa minore di un altro più piccolo di volume ma pieno o fatto di ferro.
State parlando di aria, di piume, di piombo, di ferro….di materiali diversi!
A. – La massa dipende dal materiale di cui è fatto l’oggetto.
V. e S. – Dovremmo prendere oggetti uguali per il materiale!
M. C. – Così è più facile!
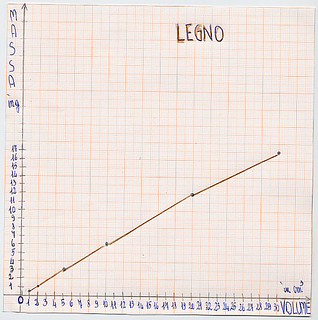
Si è operato allora con oggetti dello stesso materiale e partendo dal legno, dato che era tutto già pronto nella cassetta del materiale multibase (i cubetti delle unità, i lunghi, i piatti e i cubi v. fig. 14). Si conosceva già il volume, senza doverlo misurare e sulla bilancia si leggeva il peso, si sono registrati in tabella i dati e si è rappresentato con un grafico nel piano cartesiano.
Si è trattato di un lavoro di rappresentazione che i bambini conoscevano dalla terza per averlo fatto nei problemi di moltiplicazione …..1 leone ha 4 zampe, 2 leoni ne hanno 8, 3 leoni 12…: all’aumentare del numero dei leoni anche il numero delle zampe aumenta e aumenta con una relazione 1:4.
I bambini conoscevano anche un altro andamento. Quello ad es. del costo di una telefonata urbana ai tempi delle mamme bambine: il tempo passava, il numero dei minuti aumentava, ma il costo no. Lo stesso andamento ha la statura di un adulto al passare degli anni. (link a L’ACQUA)
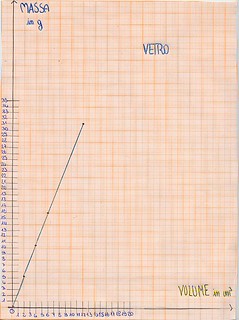
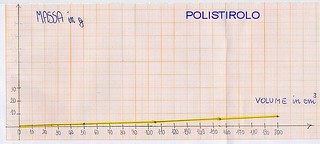
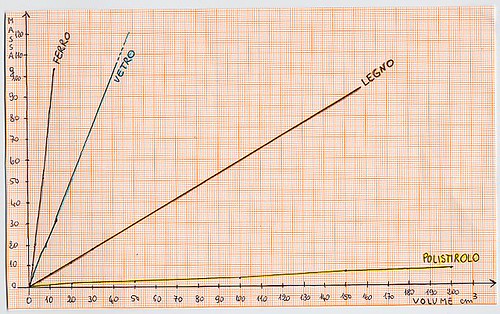
Dopo il legno si è passati al vetro, al ferro e al polistirolo. Ecco i grafici corrispondenti in fig. 15 a, b, c, d:
 |
 |
 |
 |
Già al secondo materiale, il vetro, i bambini hanno fatto previsioni e osservazioni che coglievano nel segno, come si evidenzia di seguito.
Chiedo una previsione. Si aspettano che all’aumento del volume corrisponda di nuovo un aumento della massa.
“Pensiamo che ci sarà una relazione con un andamento (!!!) più verticale rispetto al legno perché se pesi il legno e il vetro vedi che il vetro pesa di più”…avevo poco tempo e ho fatto scrivere ad un bambino ciò che volevano dire i suoi compagni: ero particolarmente soddisfatta della risposta data a voce e volevo essere certa d’aver capito bene il loro pensiero.
M. – La massa aumenta di più rispetto al legno perché in meno volume c’è più materia, c’è più vetro, ci sono più tante particelle.
N. – Mi è venuta in mente la densità di popolazione; cioè in un territorio più piccolo abitano meno persone che in uno grande, ma in proporzione sono di più.
Nicolò improvvisa uno schizzo per farmi capire (Fig. 16)
Il vetro si comporta come un materiale più pesante. E’ come se fosse più compatto, più pieno di materiale (qualcuno ha detto” dev’ essere una questione di pieno e di vuoto”), più concentrato con meno spazi vuoti dentro, più denso del legno.
Quando proviamo con il polistirolo, più nessuno sbaglia le previsioni: si aspettano che la massa aumenti poco e una linea che unisce i punti quasi orizzontale.
Osservano che succede quasi il contrario del ferro: là aumentava tanto la massa ( 5 g al cm cubo ) e poco il volume; qui poco la massa ( 0,04 g ogni cm cubo) e tanto il volume. Il polistirolo è poco concentrato, poco denso. Il polistirolo è il meno denso dei 4 materiali provati.
E’ il momento di dar retta ad Alma che aveva proposto:
“Adesso si potrebbero mettere sulla bilancia oggetti che hanno lo stesso volume fatti di materiale diverso…….”.
Abbiamo provato allora come cambia la massa in oggetti di ugual volume fatti di diverso materiale.
Ho proposto 4 cubi di ugual volume fatti di materiali diversi: legno, marmo, ferro e polistirolo.
Tutti hanno riconosciuto l’uguaglianza del volume che è stato calcolato facilmente: 64 cm cubi (quello di legno è il cubo della base quattro); tutti conoscevano bene i materiali: polistirolo ricoperto di carta sottile, legno, marmo (di Carrara), ferro (acciaio); ho chiesto di ordinarli dal meno al più pesante e abbiamo controllato con la bilancia:
| Polistirolo | legno | marmo | ferro |
| 64 cm cubi | 64 cm cubi | 64 cm cubi | 64 cm cubi |
| 3,5g | 31g | 172g | 488g |
| 1 cm cubo | 1 cm cubo | 1 cm cubo | 1 cm cubo |
| 0,05g | 0,48g | 2,6g | 7,6g |
Dalle divisioni eseguite sono risultati quozienti confrontabili con quelli che avevamo già calcolato.
Ho chiesto di immaginare come potevano essere fatti questi diversi materiali, diversi anche per la densità…. per la compattezza, per la fittezza, per come sono disposte le particelle più o meno vicine l’una all’altra.
Ho chiesto loro di mimare, di disporsi in modo adatto a farmi capire: si sono raggruppati fitti e stretti per rappresentare come dovrebbero essere disposte le particelle del ferro, un po’ meno stretti per il marmo e per il legno, ben distanziati per il polistirolo.
Ho chiesto di rappresentare disponendo granelli di farina gialla come le particelle e poi di disegnare semplicemente alla lavagna (fig. 17 a, b):
 |
 |
4 – Il galleggiamento
A fine quinta il tempo stringeva, avevamo altri percorsi da portare a termine ed era necessario concludere. Le impressioni espresse dai bambini sul lavoro svolto sono state largamente positive.
Tuttavia durante le discussioni era emerso più volte il problema del galleggiamento e si è avuta l’impressione che i bambini più pronti pensassero che cammin facendo avrebbero capito perché alcuni oggetti galleggiano e altri no. Nei messaggi di commento al lavoro infatti, qualcuno ha sottolineato di non aver ancora risolto questo problema, trovando altri dello stesso parere. In quinta A, N. è stato esplicito: ”Pensavo di imparare la relazione fra galleggiamento, volume e massa, ma non sono riuscito a capire“, ponendo un problema importante che sosteneva la motivazione e la curiosità.
Allora si è scelto di porre la questione nelle verifiche anche perché la soluzione era a portata di mano e sembrava un peccato lasciarla sfuggire.
Ci siamo accordate: Laura ha mandato una lettera ai bambini per dire a che punto stava la sua tesi, per chiedere loro di raccontare la continuazione del percorso in quinta e, sempre con il pretesto della tesi, ha sottoposto a ciascuno una tabella con l’elenco di molti oggetti che noi avevamo in classe e la richiesta di previsione/verifica riguardante il galleggiamento nell’acqua.
| oggetto |
galleggia in superficie |
sta sospeso nell'acqua |
affonda |
| 1- cubo di legno da 64 cm cubi | |||
| 2 - biglia di vetro piccola | |||
| 3 - frammento di polistirolo da 200 cm cubi | |||
| 4 - cubo di marmo da 64 cm cubi | |||
| 5 - dado di ferro | |||
| 6 - bicchiere di vetro immerso di lato | |||
| 7 - cubo di legno da 1000 cm cubi | |||
| 8 - frammento di polistirolo da 50 cm cubi | |||
| 9 - palloncino pieno d’acqua | |||
| 10 - cubo di ferro da 64 cm cubi | |||
| 11 - frammento piccolo di marmo | |||
| 12 - palloncino pieno d’olio | |||
| 13 - biglia di vetro grande | |||
| 14 - cubo di legno da 1 cm cubo |
Ognuno, da solo, ha formulato le previsioni e poi abbiamo fatto la prova di galleggiamento in una vasca colma d’acqua. (fig. 18)
Subito i ragazzi hanno notato a galla gli oggetti di legno e quelli di polistirolo, grandi o piccoli; sul fondo quelli di ferro, di vetro, di marmo grandi o piccoli.
Hanno osservano che galleggiare o affondare non è questione di volume o di massa, ma di materiale.
Si sono accorti che sono andati a fondo i materiali che erano risultati molto densi, mentre galleggiavano quelli che erano risultati meno densi. Più densi di chi e meno densi rispetto a che cosa era un passo ancora da fare.
In tutto questo percorso si è andati avanti a piccoli passi, riflettendo e ragionando anche fra una lezione e l’altra.
Si è suggerito di misurare la densità dell’acqua, dato che abbiamo misurato la densità di alcuni materiali, ma non quella dell’acqua e proposto di farlo procedendo come per gli altri 4 materiali; poiché l’acqua è liquida lo potevamo fare rapidamente mettendo direttamente sulla bilancia un contenitore graduato: abbiamo misurato contemporaneamente massa e volume.
Poi è stato preparato ai bambini il grafico di sintesi dei 4 elaborati in precedenza e insieme abbiamo registrato i dati riguardanti l’acqua (fig. 19 a, b).
 |
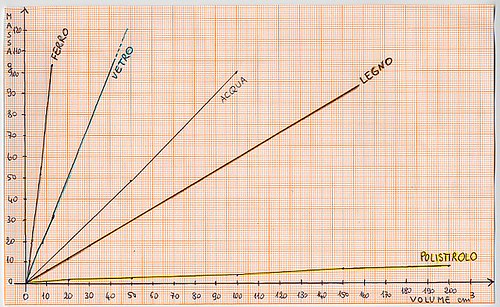 |
A colpo d’occhio i ragazzi sono illuminati dalla posizione della ”linea dell’acqua”, che divide il grafico in due parti, separando i materiali più densi dell’acqua, in alto, che affondano, da quelli meno densi dell’acqua, in basso, che galleggiano.
La conclusione immediata a questo punto è stata che galleggiare o no nell’acqua dipende dalla densità del materiale del quale un oggetto è fatto, rispetto alla densità dell’acqua.
Guardiamo insieme, per curiosità la tabella seguente:
DENSITA’ di alcuni materiali
(a 0 °C alla pressione di 1 atm)
|
Nome |
Densità (g / cm³) |
|
|
Idrogeno |
0,089 |
|
|
Elio |
0,178 |
|
|
Sughero |
0,22-0,26 |
|
|
Legno di cedro |
0,31-0,49 |
|
|
Legno di “pino bianco” |
0,35-0,50 |
|
|
Legno di quercia |
0,6-0,9 |
|
|
Benzina |
0,68 |
|
|
Alcool (etilico) |
0,806 |
|
|
Olio d'oliva |
0,92 |
|
|
Ghiaccio |
0,92 |
|
|
Acqua |
1,00 |
|
|
Acqua del mar Mediterraneo |
1,035 |
|
|
Osso |
1,7-2 |
|
|
Vetro |
2,4-2,8 |
|
|
Alluminio |
2,70 |
|
|
Cemento |
2,7-3,0 |
|
|
Ferro |
7,96 |
|
|
Rame |
8,96 |
|
|
Argento |
10,49 |
|
|
Piombo |
11,3 |
|
|
Mercurio |
13,6 |
|
|
Oro |
19,3 |
|
|
Platino |
21,37 |
|
La curiosità si riaccende ed apre nuovi argomenti. Sorgono immediate molte domande, molte idee e previsioni per prove di galleggiamento di liquidi in liquidi o di materiali vari in liquidi diversi dall’acqua (qualcosa proveremo), o nell’aria “qual è la densità dell’aria?” chiedono…
”Di quale aria?” ribatto io…umida, asciutta, calda, fredda?
E si accorgono che le cose si fanno più complesse.
E poi notano la precisazione accanto al titolo della tabella a proposito della temperatura, e la pressione che cos’è? E atm che cosa significa? Come sempre, approfondendo, si aprono discorsi e problemi nuovi.
Con il senno di poi
A percorso concluso, anche noi insegnanti abbiamo valutato il nostro lavoro e, fra le altre considerazioni che ci siamo scambiate, abbiamo riconosciuto opportuna l’osservazione di alcuni ragazzi in merito alla lentezza del procedere: due lezioni alla settimana, una di scienze e una di matematica sarebbero state l’ideale ritmo di lavoro.
Suddividere il percorso su due anni è stato per noi obbligatorio, dovendo seguire i tempi consentiti dall’università; la ricaduta sul lavoro di classe è stata positiva, perché ha permesso ai ragazzi di lasciar sedimentare le riflessioni, di guardarsi attorno, di riprovare a casa, di procedere con calma allentando con altri argomenti il filo di temi non facili, intorno ai quali si lavora comunque con andamento ricorsivo.
Il galleggiamento si è rivelato – confermando le nostre previsioni - un tema complesso. Lo si dovrebbe tuttavia affrontare anche nella scuola primaria, non solo perché incontra una motivazione fortissima, ma anche per l’importanza dei concetti e delle strategie di pensiero che mette in gioco. È opportuno però non trattarlo direttamente, ma “prenderlo un poco alla larga”, tenerlo nello sfondo, preparare il terreno, lavorare sui concetti che sono il presupposto per capire davvero.
L’ accompagnamento delle due docenti specialiste è stato un supporto per noi fondamentale, che ci ha permesso di cogliere le opportunità offerte dai temi in gioco e di evitare errori e misconcetti. L’attenzione e l’ascolto da parte loro nei confronti dei bambini e nostri sono stati cruciali per declinare la progettazione iniziale a misura delle due classi al lavoro. Per noi, è stata formazione in itinere di grande valore.
Bibliografia e sitografia essenziale
(1) Umberto Guidoni, Andrea Valente, Martino su Marte, Editoriale Scienza, Perugia, 2007
Alberti, Bozzolo, Costa, Collana Nel mondo della Matematica, Nel mondo dei Numeri e delle Operazioni e Nel mondo della Geometria, ed. Erickson
(*) Si ringrazia la prof. Carla Alberti dell’Università Cattolica di Brescia per l’assiduo e prezioso accompagnamento nello svolgimento del percorso.